Barisan dan Deret Geometri

Hari/Tanggal  : Rabu/29 juli 2020
Kelas              : 8C,8E,8F
Pahami video di atas lalu kerjakan Evaluasi Mandiri 4 halaman 24 Nomor 2A dan 2C difoto lalu kirim ke WA : 082280107255

BILANGAN BERPANGKAT NEGATIF

\

Hari/Tanggal :Selasa 28 Juli 2020
Kelas             :9A

Simak video berikut kerjakan soal latihan 3 halaman 16 nomor 4A,4E,5D,7A di buku latihan di foto alu kirim ke WA :082280107255

Barisan dan Deret Aritmatika

Hari/Tanggal:Selasa/28 Juli 2020
Kelas             :8G

Pahami video berikut kemudian kerjakan evalusi mandiri 3 halaman 19 nomor 2 dan 4 difoto kirim ke WA :082280107255

Barisan dan Deret Aritmatika

Hari/Tanggal:Senin/27 Juli 2020
Kelas             :8C,8D,8E

Pahami video berikut kemudian kerjakan evalusi mandiri 3 halaman 19 nomor 2 dan 4 difoto kirim ke WA :082280107255

MENCARI SUKU KE-N BARISAN BILANGAN

Hari/tanggal : Jum'at/24 Juli 2020
Kelas : 8F
Simak video di atas dan kerjakan Evaluasi Mandiri 2 halaman 14 nomor 1C dan 2B di buku latihan difoto lalu kirim ke WA: 082280107255

Bilangan Berpangkat Positif

Hari/tanggal : Jumat/2 september 2022
Kelas : 7A
Simak video di atas dan kerjakan Latihan 1.2 halaman 20 nomor 1A,1D,3B dan Latihan 1.3 halaman 30 nomor 1A dan 1F di buku latihan difoto lalu kirim ke WA: 082280107255 

MENCARI SUKU KE-N BARISAN BILANGAN

Hari/tanggal : Kamis/23 Juli 2020
Kelas : 8D dan 8G
Simak video di atas dan kerjakan Evaluasi Mandiri 2 halaman 14 nomor 1A,1B,2A,2F di buku latihan difoto lalu kirim ke WA: 082280107255 

MENENTUKAN SUKU KE-N BARISAN BILANGAN

Hari/tanggal : Rabu/22 Juli 2020
Kelas : 8C,8E,8F
Simak video di atas dan kerjakan Evaluasi Mandiri 2 halaman 14 nomor 1A,1B,2A,2F di buku latihan difoto lalu kirim ke WA: 082280107255 paling lambat pukul 15.00

NOTASI ILMIAH

HARI/TANGGAL : SELASA/21 JULI 2020

KELAS : 9A

PAHAMI MATERI NOTASI ILMIAH HALAMAN 8 DAN KERJAKAN LATIHAN 1 HALAMAN 9 NOMOR 7A,7F,8A,8D LALU FOTO DAN KIRIM KE 

WA : 082280107255 PALING LAMBAT PUKUL 16.00

Pola Bilangan

Hari/tanggal : Selasa/21 Juli 2020

Kelas : 8G

Pahami pola bilangan pada buku paket Dikbud Tiga Serangkai kemudian jawablah pertanyaan berikut pada buku latihan lalu foto dan kirim WA : 082280107255 paling lambat pukul 15.00 

Kegiatan 1

1.   Amati gambar berikut. Tuliskan banyaknya persegi kecil pada setiap bangun.
   
2. Dapatkah kalian menemukan pola keteraturan? Dengan pola tersebut gambarkan bangun berikutnya dan tuliskan banyaknya persegi kecil di bawah gambar
   
3. Tanpa menggambar dapatkah kalian menentukan banyaknya persegi kecil untuk bangun berikutnya?                                       Jawab :  .... , ....., ......, ..... , ..... , ..... , ..... , .....
4. Tanpa menggambar dapatkan kalian menemukan banyaknya persegi kecil pada bangun yang ke-20?  Jawab : 
   

     

Catatan: pola bilangan yang kalian temukan disebut pola bilangan persegi

Pola Bilangan

Hari/tanggal : Senin/20 Juli 2020

Kelas : 8C,8D,8E

Pahami pola bilangan pada buku paket Dikbud Tiga Serangkai kemudian jawablah pertanyaan berikut pada buku latihan lalu foto dan kirim WA : 082280107255 paling lambat pukul 15.00 

Kegiatan 1

1.   Amati gambar berikut. Tuliskan banyaknya persegi kecil pada setiap bangun.
   
2. Dapatkah kalian menemukan pola keteraturan? Dengan pola tersebut gambarkan bangun berikutnya dan tuliskan banyaknya persegi kecil di bawah gambar
   
3. Tanpa menggambar dapatkah kalian menentukan banyaknya persegi kecil untuk bangun berikutnya?                                       Jawab :  .... , ....., ......, ..... , ..... , ..... , ..... , .....
4. Tanpa menggambar dapatkan kalian menemukan banyaknya persegi kecil pada bangun yang ke-20?  Jawab : 
   

     

Catatan: pola bilangan yang kalian temukan disebut pola bilangan persegi

Kegiatan Siswa

Hari/tanggal : Jum'at/17 Juli 2020

Kelas : 8F

Pahami pola bilangan pada buku paket kemudian jawablah pertanyaan berikut pada buku latihan lalu foto dan kirim WA : 082280107255 paling lambat pukul 15.00 

Kegiatan 3

1.        Amati gambar berikut dan gambarlah bangun berikutnya pada titik-titik yang disediaka 

  

2.        Hitunglah banyaknya persegi pada masing-masing gambar yang telah kalian gambar pada langkah 1. Tuliskan dalam barisan bilangan berikut.

Jawab :

1, 3, 6, 10, 15, ..... , .... 

3.        Tanpa menggambar dapatkah kalian menentukan banyaknya persegi untuk bangun segitiga berikutnya?

Jawab :

1, 3, 6, 10, 15, ..... , ..... , ..... , ..... , .....    

4.        Bandingkan hasil pada 3 dengan barisan yang telah kalian temukan pada langkah 2, apakah pola bilangan membentuk pola bilangan segitiga?

Kegiatan 4

1.        Amati gambar berikut dan gambarlah bangun berikutnya

 

2.        Hitunglah banyaknya titik pada masing-masing gambar yang telah kalian gambar pada langkah 1. Tuliskan dalam barisan bilangan berikut.

Jawab :

2, 6, 12, 20, 30, ..... , .... 

3.        Tanpa menggambar dapatkah kalian menentukan banyaknya titik untuk bangun berikutnya?

Jawab :

2, 6, 12, 20, 30, ..... , ..... , ..... , ..... , .....

4.        Hitunglah banyaknya titik berwarna hijau saja pada masing-masing bangun.

Jawab :

...., .... , ...., ...., ..... , ..... , ..... , ..... , .....

5.        Bandingkan hasil pada 3 dengan barisan yang telah kalian temukan pada kegiatan 2 dan 3

no 3, apakah pola bilangan membentuk pola bilangan segitiga?Jelaskan.

Jawab :

..............................................................................................................................................................................................................................................................................................................................................................................................................................................................................

6.        Gambarkan dengan bahasamu pola bilangan segitiga

Jawab:

BILANGAN BERPANGKAT

Hari/Tanggal:kAMIS/16 Juli 2020

Kelas :9A

Pahami materi berikut dan kerjakan latihan 1 halaman 9 nomor 3b,3d,6b,6e di buku latihan kemudian foto kirim ke WA  082280107255 paling lambat jam 13.00

Bilangan Berpangkat

Bilangan berpangkat merupakan suatu bilangan yang berguna untuk menyederhanakan penulisan serta penyebutan suatu bilangan yang mempunyai faktor-faktor perkalian yang sama.

Sebagai contoh: 3x3x3x3x3=… atau 7x7x7x7x=… , dan lain sebagainya.

Perkalian berbagai bilangan dengan faktor-faktor yang sama seperti di atas pada umumnya disebuat dengan perkalian berulang.

Bayangkan apabila yang dikalikan angkanya sangat banyak, maka kita juga akan mengelami kesulitan di dalam dalam penulisannya.

Hal tersebut tak lain sebab sangking banyaknya angka untuk satu kali bilangan pada perkalian tersebut.

Masing-masing perkalian berulang bisa kita tuliskan secara ringkas dengan memakai notasi angka bilangan berpangkat.

Sebagai contoh:

3 x 3 x 3 x 3 x 3 bilangan tersebut bisa kita ringkas kembali dengan memakai bilangan berpangkat menjadi 35

8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 dan angka tersebut bisa kita ringkas kembali hingga menjadi bilangan berpangkat 810

Cara membacanya:

35: Sepuluh pangkat 5

 810 : Delapan pangakt 10

Pangkat di atas berguna untuk menentukan jumlah faktor yang di ulang.

Rumus bilangan berpangkat yaitu:

an=a×a×a×a…sebanyak n kali

Jenis  Jenis Bilangan Berpangkat

Terdapat beberapa jenis bilangan berpangkat yang paling sering dibahas.

Antara lain yakni: bilangan berpangkat positif (+), bilangan berpangkat negatif (-) serta bilangan berpangkat nol (0).

Berikut akan kami berikan penjelasan pada masig-masing jenisnya. Simak baik-baik ulasan di bawah ini ya.

1. Bilangan Berpangkat Positif

Bilangan berpangkat positif merupakan suatu bilangan yang mempunyai pangkat atau eksponen positif.

Apa itu yang dimaksud sebagai eksponen? eksponen merupakan penyebutan lain dari pangkat. Bilangan berpangkat positif mempunyai sifat-sifat tertentu, yang mana bilangan tersebut terdiri atas a, b, sebagai bilangan real dan m, n, yang merupakan bilangan bulat positif.

Bilangan Eksponen merupakan suatu bentuk pada bilangan perkalian dengan bilangan yang sama kemudian di ulang-ulang atau pengertian singkatnya yaitu perkalian yang diulang-ulang.

Adapun beberapa sifat dari bilangan berpangkat positif, diantaranya ialah sebagai berikut ini:

1. am x an = am+n
2. am : an = am-n , untuk m>n dan b ≠ 0
3. (am)n = amn
4. (ab)m = am bm
5. (a/b)m = am/bm , untuk b ≠ 0

Untuk lebih memahami uraian di atas, perhatikan baik-baik contoh soal di bawah ini.

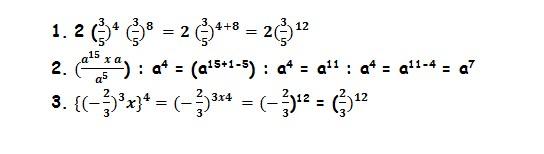
2. Bilangan Berpangkat Negatif

Kemudian ialah pengertian dari bilangan berpangkat negatif yang merupakan bilangan yang mempunyai pangkat atau eksponen negatif (-).

Adapun beberapa sifat bilangan berpangkat negatif, antara lain ialah sebagai berikut:

Jika a∈R, a ≠ 0, dan n merupakan bilangan bulat negatif, maka:

a-n = 1/an atau an = 1/ a-n

Untuk lebih memahami uraian di atas, perhatikan baik-baik contoh soal di bawah ini:

Soal 1.

Tentukan sekaligus nyatakan dengan pangkat positif bilangan berpangkat di bawah ini:

1/ 6(a + b)-7 = ….

Jawab:

1/ 6(a + b)-7 = = 1/6 (a+b)7

Soal 2.

Nyatakan dengan pangkat negatif bilangan berpangkat di bawah ini:

x1y2 / 2z6 = ….

Jawab:

x1y2 / 2z6 = 2-1x-1z-6 / y-2, dengan x ≠ 0 dan z ≠ 0.

3. Bilangan berpangkat Nol (0)

Tak hanya ada bilangan berpangkat positif serta bilangan berpangkat negatif yang ada pada bilangan berpangkat lho.

Ternyata, dalam ilmu matematika juga terdapa bilangan berpangkat nol (a). Maka dati itu, yuk mari kita pelajari lebih dalam mengenai bilangan berpangkat nol ini.

Sebelumnya kita sudah mengetahui bahwa sifat-sifat bilangan berpangkat, ialah sebagai berikut:

an/an = 1 berdasarkan dari sifat pembagian bilangan berpangkat positif maka bisa kita dapatkan:

an/an = an-n = a0, sehingga a0 = 1

Sehingga sifat dari bilangan berpangkat nol (0) yaitu “Jika nilai a merupakan bilangan riil serta a tidak sama dengan 0, maka a0 = 1″

Untuk lebih memahami uraian di atas, perhatikan baik-baik contoh soal di bawah ini:

Sederhanakan beberapa bilangan berpangkat di bawah ini:

Soal 1.

5(x2 – y2)(x2 – y2)0

Soal 2.

3x + 2 y / (3x + 2y)0

Jawab:

Soal 1.

5(x2 – y2)(x2 – y2)0 = 5(x2 – y2) x 1 = 5(x2 – y2), dengan x2 – y2  ≠ 0

Soal 2.

3x + 2 y / (3x + 2y)0 = 3x + 2y / 1 = 3x + 2y, dengan 3x + 2y ≠ 0

Demikianlah pembahasan yang dapat kita sampaikan terakti bilangan berpangkat, sekarang kita lanjutkan ke pembahasan yang ke dua yakni Bentuk Akar. Perhatikan baik-baik ulasan di bawah ini ya..

Sifat Sifat Bilangan Berpangkat

Berikut ini adalah beberapa sifat yang terdapat di dalam bilangan berpangkat, antara lian yakni:

1. Pangkat Bulat positif

Pengertian:

Sebagai contohnya a bilangan real serta n bilangan bulat positif. Notasi anakan menyatakan hasil kali dari bilangan a sebanyak n faktor. Sehingga dapat kita tuliskan menjadi:

an = a × a × a × … × a

Di mana : a x a x a x …. x a merupakan n faktor.

Keterangan:

• a merupakan basis bilangan berpangkat.
• n merupakan pangkat.

Sehingga, dapat kita ketahui bahwa:

1. Pada uraian di atas, maka kita sepakati, a1 cukup ditulis dengan a.
2. Tidak seluruh a0 dengan a bilangan real menyatakan 1. Pada saat a = 0 serta n = 0, maka an= 00, maka hasilnya tidak menentu.
3. Apabila n merupakan suatu variabel sebagai eksponen dari a, maka perlu kita perhatikan semesta variabel tersebut.
   Karena an = a × a × … × a sebanyak n faktor, ini hanya berlaku pada saat semesta n ∈N.

Untuk lebih memahami uraian di atas, perhatikan baik-baik contoh soal di bawah ini:

1. 24 = 2 x 2 x 2 x 2 =16
2. 32 = 3 x 3 = 9

2. Pangkat Bulat Negatif

Pengertian:

Untuk a bilangan real serta a ≠ 0, m bilangan bulat positif, maka di definisikan menjadi:

a-m = (1/a)m

Dari uraian di atas maka dapat dijelaskan lagi menjadi sebagai berikut:

Untuk lebih memahami uraian di atas, perhatikan baik-baik contoh soal di bawah ini:

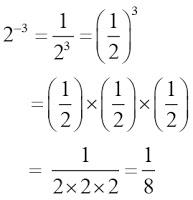
3. Pangkat Nol

Pengertian:

Untuk a bilangan real serta a ≠ 0, maka a0 = 1.

Kenapa a tidak boleh sama dengan nol?

Seperti yang sudah dijelaskan di atas, pada saat a = 0 maka a0 = 00, maka hasil­nya tidak menentu.

Sebagai contoh:

• 20 = 1
• 30 = 1

4. Sifat-sifat Pangkat Bulat Positif

Berikut adalah beberapa sifat dari bilangan pangkat bulat positif:

Sifat-1

Apabila a bilangan real, m serta n bilangan bulat positif maka

am × an = am+n

Pembuktian:

Si­fat di atas hanya berlaku apabila a merupakan bilangan real, m serta n merupakan bi­langan bulat positif. Apabila m dan n bukan bilangan bulat positif, maka sifat-1 tidak berlaku. Contohnya: a = 0 dan m = n = 0, tidak ber­laku.

Sebagai contoh:

22 x 23 = (2 x 2) x (2 x 2 x 2)

= 32

= 25

22 x 23 = 22+3

Sifat-2

Apabila a bilangan real serta a ≠ 0, m dan n bilangan bulat positif, sehingga:

Dalam sifat-2 tidak diperkenakan apabila a = 0, karena ben­tuk perpangkatan pada sifat-2 merupakan bentuk ra­sional.

Pada pecahan yang penyebutnya tidak lazim nol. Pada a = 0 dan m, n merupakan bilangan bulat positif, sehingga am atau an dimung­kinkan hasilnya 0.

Apabila hasil am serta an keduanya nol, maka hasil baginya tidak menentu.

Apabila am = 0 dan an ≠ 0, maka hasil baginya 0. Namun, apabila am ≠ 0 dan an = 0, maka hasil baginya tak ter­definisi.

Sebagi contoh:

25 / 23 = 2 x 2 x 2 x 2 x 2 / 2 x 2 x 2

= 4

= 22

= 25-3

Perpangkatan Bilangan Bulat

Secara umum, perkalian sembarang bilangan bulat a sebanyak n kali atau n faktor, yaitu:

a × a × a × … × a atau jika ditulis menjadi an

Keterangan:

a = disebut sebagai bilangan pokok atau bilangan dasar
n = disebut sebagai pangkat atau eksponen
an = disebut sebagai bilangan berpangkat (dibaca a pangkat n)

Sifat-3

Jika a bilangan real serta a ≠ 0, m dan n merupakan bilangan bulat positif, maka (am)n = amn

Pembuktian:

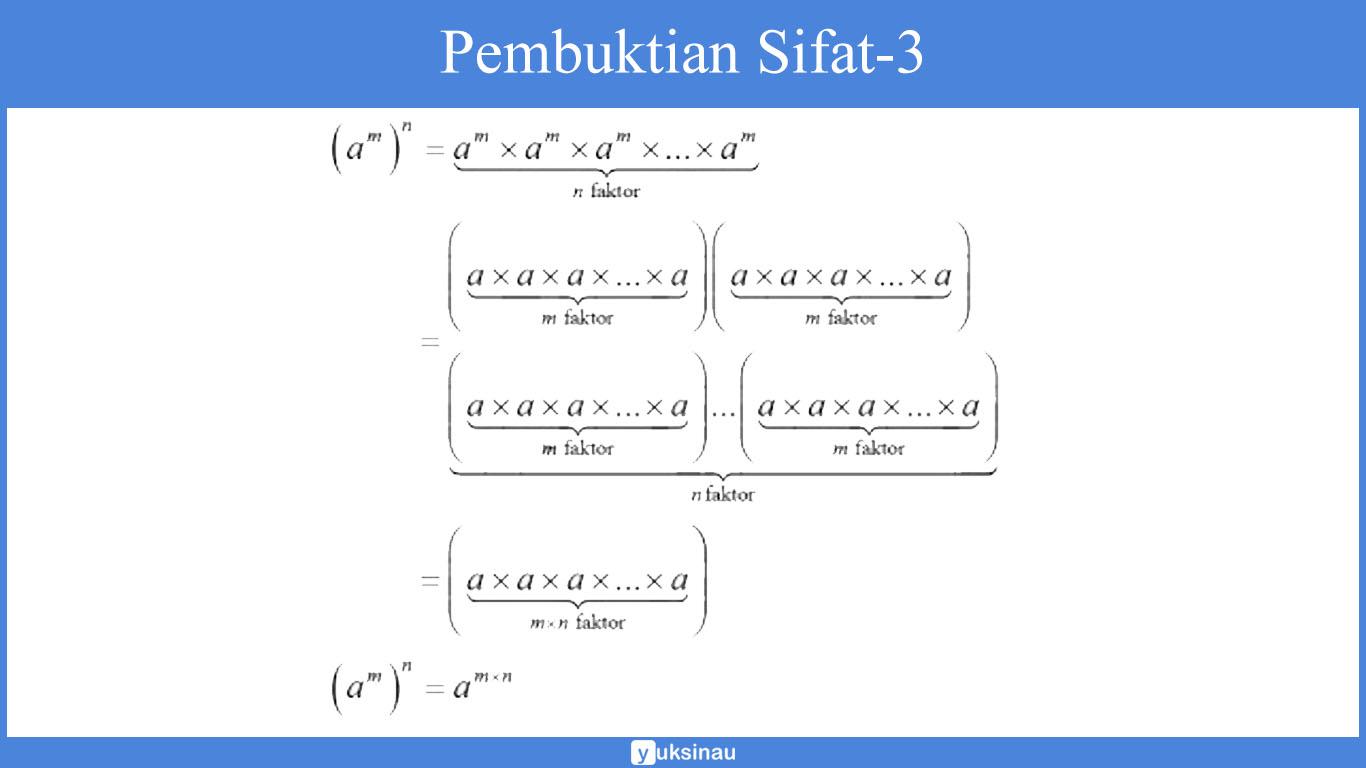
Sebagi contoh:
(23)2 = (23) x (23)

= (2 x 2 x 2) x (2 x 2 x 2)

= 2 x 2 x 2 x 2 x 2 x 2

= 26

Di mana (2 x 2 x 2) merupakan 3 faktor, 2 x 2 x 2 x 2 x 2 x 2 merupakan 6 faktor, dan lain sebagainya.

5. Pangkat Pecahan

Pengertian:

Contohnya a merupakan bilangan real dan a ≠ 0, serta m merupakan bilangan bulat positif, maka a1/m = p merupakan bilangan real positif, sehingga pm = a.

Sifat-sifat perpangkatan bilangan real dengan pangkat pecahan

Pengertian:

Contonya a merupakan bilangan real dan a ≠ 0, m, n merupakan bilangan bulat positif maka didefinisikan menjadi:

am/n = (a1/n)m

Misalkan a merupakan bilangan real dengan a > 0,

p/n dan m/n merupakan bilangan pecahan n ≠ 0, maka:

(am/n) = (ap/n) = (a)m+p/n