MATEMATIKA ITU MUDAH

Kamis, 31 Oktober 2019

Hari/tanggal: Jum'at/1 November 2019
Kelas: 9A-9B

Langkah-langkah menggambar grafik fungsi kuadrat:

Tentukan titik potong dengan sumbu x (nilai y atau f(x) sama dengan 0).
Tentukan titik potong dengan sumbu y (nilai x = 0).
Menentukan sumbu simetri $x= -\frac{b}{2a}$ .
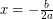Menentukan titik puncak ( $-\frac{b}{2a}$ , $-\frac{b^{2} - 4ac}{4a}$ ) atau hitung nilai puncak y menggunakan substitusi/mengganti nilai x yang diperoleh pada perhitungan nomor 3 ke dalam persamaan f(x).

Contoh Soal dan Pembahasan

$y = x^{2} - 2x - 8$

Nilai $a = 1 > 0$ artinya grafik akan terbuka ke atas.
Nilai 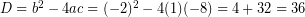$D = b^{2} - 4ac = (-2)^{2} - 4(1)(-8) = 4 + 32 = 36$ , nilai D > 0 artinya grafik akan memotong sumbu x pada dua titik.

Sketsa Grafik Persamaan Kuadrat

Langkah 1:

$y=0$

$x^{2} - 2x - 8 = 0$

$(x-4)(x+2) = 0$

$x = 4 \textrm{ atau } x = -2$

Langkah 1

Langkah 2:

$y = x^{2} - 2x - 8$

$y = 0^{2} - 0 - 8$

$y = - 8$

Langkah 2

Langkah 3:

$x = -\frac{b}{2a}$

$y = x^{2} - 2x - 8$

$a = 1$

$b = -2$

$c = -8$

$x = -\frac{-2}{2} = 1$

Langkah 3

Langkah 4:

$-\frac{b}{2a}$

$-\frac{b^{2} - 4ac}{4a}$

$x = -\frac{b}{2a} = -\frac{-2}{2} = 1$

$y=-\frac{b^{2} - 4ac}{4a}=-\frac{(-2)^{2} - 4(1)(-8)}{4(1)} = -\frac{36}{4}=-9$

$y = x^{2} - 2x - 8$

$y = 1^{2} - 2(1) - 8$

$= 1 - 2 - 8 = - 9$

Langkah 4a

Selanjutnya tinggal menghubungkan titik-titik yang diperoleh sehingga menjadi kurva mulus seperti terlihat pada gambar berikut.

Grafik fungsi kuadrat

Grafik fungsi kuadrat

Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)