Hari/tanggal: Kamis/14 November 2019
Kelas: 9A/9B
Fungsi Kuadrat
Fungsi kuadrat adalah suatu persamaan dari variabel yang mempunyai pangkat tertinggi dua. Fungsi ini berkaitan dengan
persamaan kuadrat. Bentuk umum persamaan kuadrat adalah:
Sedangkan bentuk umum dari fungsi kuadrat adalah:
Dengan a, b, merupakan koefisien, dan c adalah konstanta, serta

.
Fungsi kuadrat f(x) dapat juga ditulis dalam bentuk y atau:
Dengan x adalah variable bebas dan y adalah variable terikat. Sehingga nilai y tergantung pada nilai x, dan nilai-nilai x tergantung pada area yang ditetapkan. Nilai y diperoleh dengan memasukan nilai-nilai x kedalam fungsi.
Grafik Fungsi Kuadrat
Fungsi kuadrat

dapat digambarkan ke dalam koordinat kartesius sehingga diperoleh suatu grafik fungsi kuadrat. Sumbu x adalah domain dan sumbu y adalah kodomain. Grafik dari fungsi kuadrat berbentuk seperti parabola sehingga sering disebut grafik parabola.
Grafik dapat dibuat dengan memasukan nilai x pada interval tertentu sehingga didapat nilai y. Kemudian pasangan nilai (x, y) tersebut menjadi koordinat dari yang dilewati suatu grafik. Sebagai contoh, grafik dari fungsi:
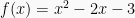
adalah:


Jenis grafik fungsi kuadrat lain
1. Grafik fungsi 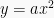
Jika pada fungsi

memiliki nilai b dan c sama dengan nol, maka fungsi kuadratnya:
Pada grafik fungsi ini akan selalu memiliki garis simetris pada x = 0 dan titik puncak y = 0. Sebagai contoh
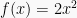
, maka grafiknya adalah:

2. Grafik fungsi 
Jika pada fungsi

memiliki nilai b = 0, maka fungsi kuadratnya sama dengan:
Pada fungsi ini grafik akan memiliki kesamaan dengan grafik fungsi kuadrat
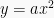
yaitu selalu memiliki garis simetris pada x = 0. Namun, titik puncaknya sama dengan nilai c atau
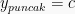
. Sebagai contoh =

+ 2, maka grafiknya adalah:

3. Grafik fungsi 
Grafik ini merupakan hasil perubahan bentuk dari

. Pada fungsi kuadrat ini grafik akan memiliki titik puncak (x, y) sama dengan (h, k). Hubungan antara a, b, dan c dengan h, k sebagai berikut:
Sifat-sifat Grafik Fungsi Kuadrat
a. Grafik terbuka
Grafik

dapat terbuka ke atas atau ke bawah. Sifat ini ditentukan oleh nilai a. Jika
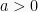
maka grafik terbuka ke atas, jika

maka grafik terbuka kebawah.

b. Titik Puncak
Grafik kuadrat mempunyai titik puncak atau titik balik. Jika grafik terbuka kebawah, maka titik puncak adalah titik maksimum. Jika grafik terbuka keatas maka, titik puncak adalah titik minimum.
c. Sumbu Simetri
Sumbu simetri membagi grafik kuadrat menjadi 2 bagian sehingga tepat berada di titik puncak. Karena itu, letaknya pada grafik

berada pada:
d. Titik potong sumbu y
Grafik

memotong sumbu y di x = 0. Jika nilai x = 0 disubstitusikan ke dalam fungsi, diperoleh y = c. Maka titik potong berada di (0, c).

e. Titik potong sumbu x
Grafik kuadrat akan memotong sumbu x di y = 0, sehingga membentuk persamaan:
Akar-akar dari persamaan tersebut adalah absis dari titik potong. Oleh karena itu, nilai diskriminan (D) berpengaruh pada keberadaan titik potong sumbu x sebagai berikut:
- Jika
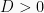 , grafik memotong sumbu x di dua titik
, grafik memotong sumbu x di dua titik
- Jika
 , grafik menyinggung sumbu x
, grafik menyinggung sumbu x
- Jika
 , grafik tidak memotong sumbu x
, grafik tidak memotong sumbu x
Jika digambarkan, sebagai berikut:

Menyusun Persamaan Grafik Fungsi Kuadrat
Persamaan grafik fungsi kuadrat dapat dibentuk dengan syarat:
- Diketahui tiga titik koordinat (x, y) yang dilalui oleh grafik
Ketiga koordinat tersebut, masing-masing disubstitusikan kedalam persamaan grafik:
Sehingga didapat tiga persamaan berbeda yang saling memiliki variabel a, b dan c. Selanjutnya dilakukan teknik eliminasi aljabar untuk memperoleh nilai dari a, b dan c. Setelah diperoleh nilai-nilai itu, kemudian masing-masing disubstitusikan ke dalam persamaan

sebagai koefisien.
- Diketahui titik potong dengan sumbu x dan satu titik yang dilalui
Jika titik potong sumbu x adalah
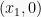
dan
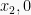
, maka rumus fungsi kuadrat nya adalah:
Dengan nilai a didapat dari mensubstitusikan titik (x, y) yang dilalui.
- Diketahui titik puncaknya dan satu titik yang dilalui
Jika titik puncaknya adalah
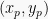
, maka rumus fungsi kuadrat nya adalah:
Dengan nilai a didapat dari mensubstitusikan titik (x, y) yang dilalui.
Contoh Soal Fungsi Kuadrat dan Pembahasan
Contoh Soal 1
Jika grafik

mempunyai titik puncak (1, 2), tentukan nilai a dan b. (UMPTN ’92)
Pembahasan 1:
Gunakan rumus
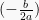
sebagai nilai x titik puncak, sehingga:
Substitusi titik puncak (1, 2) ke dalam persamaan

diperoleh:
Dari persamaan baru, substitusikan nilai

,maka:
Contoh Soal 2
Jika fungsi
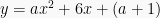
mempunyai sumbu simetri x = 3, tentukan nilai maksimumnya. (UMPTN ‘00)
Pembahasan:
Sumbu simetri berada di x titik puncak, sehingga:
Sehingga fungsi y menjadi:
Nilai maksimumnya:
Soal 3
Tentukan grafik yang melintasi (-1, 3) dan titik minimumnya sama dengan puncak grafik
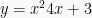
. (UMPTN ‘00)
Pembahasan:
Titik puncak

adalah:
Substitusikan nilai
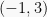
dan
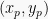
dalam persamaan:
Maka grafik fungsi kuadrat yang dicari adalah:
sumber: https://www.studiobelajar.com/fungsi-kuadrat/

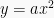






, grafik memotong sumbu x di dua titik
, grafik menyinggung sumbu x
, grafik tidak memotong sumbu x



Tidak ada komentar:
Posting Komentar