Hari/Tanggal : Kamis/4 Juni 2020Kelas : 8D-8G
MATERI PAS KELAS 8
GARIS SINGGUNG LINGKARAN
Ulasan materi terkait garis singgung lingkaran yang pertama akan dibahas adalah garis singgung persekutuan luar dua lingkaran. Persamaan garis singgung lingkaran persekutuan luar melibatkan dua lingkaran dan sebuah garis singgung lingkaran. Untuk lebih jelasnya dapat dilihat pada gambar di bawah.
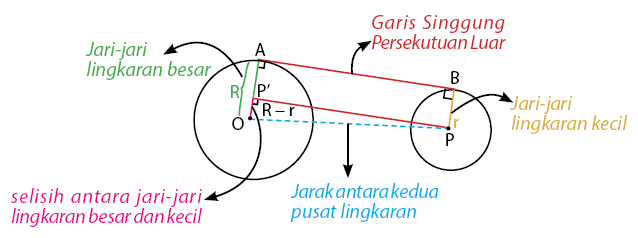
Garis AB adalah garis singgung persekutuan luar dua lingkaran. Konsep untuk mengetahui panjang garis singgung persekutuan luar dua lingkaran adalah teorema pythagoras. Langkah pertama adalah proyeksikan titik P ke garis OA. Panjang garis PP’ sama dengan garis AB, sehingga dengan menghitung panjang PP’ maka kita juga akan mendapatkan panjang AB (garis singgung persekutuan dua lingkaran).
Perhatikan bahwa segitiga PP’O merupakan segitiga siku-siku yang siku-siku di P’. Dengan teorema phytagoras dapat diperoleh panjang PP’ yaitu sebagai berikut. ![Rendered by QuickLaTeX.com \[ PP' = \sqrt{OP^{2}-\left( OP'\right)^{2}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-0f6d507ed636becc2ad2fe97e815c860_l3.png)
Karena  maka,
maka, ![Rendered by QuickLaTeX.com \[ PP' = \sqrt{OP^{2} - \left( R - r\right)^{2}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-6f6807b7580568961ad1dbda5d5d0fa3_l3.png)
Sehingga, rumus garis singgung persekutuan luar dua llingkaran dapat dinyatakan dalam rumus di bawah.
Rumus mencari panjang garis singgung persekutuan luar dua lingkaran: ![Rendered by QuickLaTeX.com \[ AB = PP' = \sqrt{OP^{2}-(R-r)^{2}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-e3287382bcab3661c25486ef3a1e5cea_l3.png)
Keterangan:
AB = PP’ = Garis singgung persekutuan luar lingkaran
OP = Jarak antara kedua pusat lingkaran
R = Jari-jari lingkaran besar
r = jari-jari lingkaran kecil
Selanjutnya simak bentuk garis singgung lingkaran yang lainnya, yaitu garis singgung persekutuan dalam dua lingkaran.
Seperti halnya garis singgung persekutuan luas dua lingkaran, garis singgung persekutuan dalam dua lingkaran juga melibatkan dua buah lingkaran dan sebuah garis singgung. Bedanya terletak pada posisi garis singgung lingkaran. Dua titik singgung lingkaran pada garis singgung persekutuan luar dua lingkaran terletak di sisi yang sama. Sedangkan dua titik singgung lingkaran pada garis singggung persekutuan dalam dua lingkaran terletak bersebrangan. Untuk lebih jelasnya, perhatikan gambar di bawah!
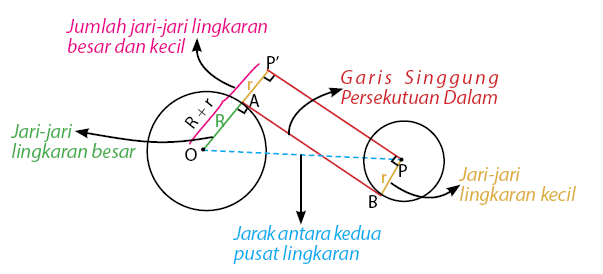
Sama halnya dengan garis singgung persekutuan dalam, garis singgung persekutuan luar juga didapat dengan menerapkan konsep teorema phytagoras.
Perhatikan bahwa segitiga PP’O merupakan segitiga siku-siku yang siku-siku di P’. Dengan teorema phytagoras dapat diperoleh panjang PP’ yaitu sebagai berikut. ![Rendered by QuickLaTeX.com \[ PP' = \sqrt{OP^{2}-\left( OP'\right)^{2}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-0f6d507ed636becc2ad2fe97e815c860_l3.png)
Karena 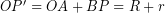 maka,
maka, ![Rendered by QuickLaTeX.com \[ PP' = \sqrt{OP^{2} - \left( R + r\right)^{2}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-43b0f52f642141ac52b6afd1b264c385_l3.png)
Sehingga, rumus garis singgung persekutuan dalam dua llingkaran dapat dinyatakan dalam rumus di bawah.
Rumus mencari panjang garis singgung persekutuan dalam ![Rendered by QuickLaTeX.com \[ AB = PP' = \sqrt{OP^{2} - (R + r)^{2}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-d9bbc516875d78adeb05d4951a45b58f_l3.png)
Keterangan:
AB = PP’ = Garis singgung persekutuan luar lingkaran
OP = Jarak antara kedua pusat lingkaran
R = Jari-jari lingkaran besar
r = jari-jari lingkaran kecil
Begitulah rumus mencari garis singgung lingkaran yang melibatkan dua lingkaran. Selanjutnya, sobat idschool dapat menyimak contoh soal garis singgung persekutuan luar lingkaran dan garis singgung persekutuan dalam lingkaran.
Contoh Soal Garis Singgung Persekutuan Luar Dua Lingkaran (SOAL UN Matematika SMP 2016)
Dua buah lingkaran memiliki panjang garis singgung persekutuan luar 24 cm dan jarak kedua titik pusat lingkaran 26 cm. Jika panjang jari-jari lingkaran besar 18 cm, maka panjang jari-jari lingkaran yang lain adalah ….
A. 6 cm
B. 8 cm
C. 9 cm
D. 10 cm
Pembahasan:
Berdasarkan data pada soal, kita dapat peroleh gambar di bawah.

![Rendered by QuickLaTeX.com \[AB =\sqrt{OP^{2}-\left( R - r\right)^{2}}\]](https://idschool.net/wp-content/ql-cache/quicklatex.com-6746535a6d320a62501e3cdf7d827d5c_l3.png)
![Rendered by QuickLaTeX.com \[AB^{2} =OP^{2}-\left( R - r\right)^{2}\]](https://idschool.net/wp-content/ql-cache/quicklatex.com-d6907fd92021b94b62b6021d3b13fbac_l3.png)
![Rendered by QuickLaTeX.com \[24^{2} =26^{2}-\left( 18 - r\right)^{2}\]](https://idschool.net/wp-content/ql-cache/quicklatex.com-212a56d23226913f21ba2caceee945b2_l3.png)
![Rendered by QuickLaTeX.com \[676 =576 - \left( 18 - r\right)^{2}\]](https://idschool.net/wp-content/ql-cache/quicklatex.com-4bdef9533bf5206a1fdca67f98b22c67_l3.png)
![Rendered by QuickLaTeX.com \[\left( 18 - r\right)^{2} =676 - 576 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-9f03af5df3fb1e6a1aaf1fd993dd0dbf_l3.png)
![Rendered by QuickLaTeX.com \[\left( 18 - r\right)^{2} = 100 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-3ffdd389cd122d3a73e17c850f3e5e61_l3.png)
![Rendered by QuickLaTeX.com \[ 18 - r = 10 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-7addb3fe67d3a4607bc4ae388c7a9838_l3.png)
![Rendered by QuickLaTeX.com \[ - r = 10 -18 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-869fef16c5414102fd8d720196bb14a0_l3.png)
![Rendered by QuickLaTeX.com \[ - r = -8 \rightarrow r = 8 \; cm \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-bf210cdc151e78e41cecef5085d5c278_l3.png)
Jadi, panjang jari-jari lingkaran yang lain adalah 8 cm.
Jawaban: D
Contoh Soal Garis Singgung Persekutuan Dalam Dua Lingkaran
Perhatikan gambar berikut!

Panjang jari-jari lingkaran besar dan kecil berturut-turut adalah 10 cm dan 5 cm. Jarak kedua pusat lingkaran adalah 25 cm. Panjang garis singgung AB adalah ….
A. 12 cm
B. 15 cm
C. 17 cm
D. 20 cm
Pembahasan: ![Rendered by QuickLaTeX.com \[ AB = \sqrt{OP^{2} - PC^{2}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-ea3f31891abd305017c7924bc54aefb6_l3.png)
![Rendered by QuickLaTeX.com \[ AB = \sqrt{OP^{2} - \left( R + r\right)^{2}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-7358cd3b9f28bf8c648bc040db70bd2e_l3.png)
![Rendered by QuickLaTeX.com \[ AB = \sqrt{25^{2} - \left( 10 + 5\right)^{2}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-a228ea461f6a183b5248d0c628d68f49_l3.png)
![Rendered by QuickLaTeX.com \[ AB = \sqrt{625 - 225} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-c5868616d8e2476a5e0a7f9d7836299e_l3.png)
![Rendered by QuickLaTeX.com \[ AB = \sqrt{400} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-c9122efddcab2bcf7da50c0baf5fe7e3_l3.png)
![Rendered by QuickLaTeX.com \[ AB = 20 \; cm \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-dafc8e538ba8d9127e12971fc15ff4e0_l3.png)
Jawaban: D sumber : https://idschool.net/smp/garis-singgung-lingkaran/


Tidak ada komentar:
Posting Komentar