TABUNG

 

 HARI/TANGGAL:SENIN/1 MARET 2021

MATA PELAJARAN:MATEMATIKA

KELAS                  :9A

A.KOMPETENSI DASAR

 3.7 Membuat generalisasi luas permukaan dan volume berbagai bangun ruang sisi lengkung (tabung, kerucut, dan bola)

B.TUJUAN PEMBELAJARAN

 Siswa diharapkan dapat :

 ·      Membuat generalisasi luas permukaan dan volume bangun ruang sisi lengkung tabung

·      Membuat generalisasi luas permukaan dan volume bangun ruang sisi lengkung kerucut

·      Membuat generalisasi luas permukaan dan volume bangun ruang sisi lengkung bola

C.APERSEPSI

Assalamualaikum wr.wb anak-anak soleh-solehah bagaimana khabarnya hari ini sudah sholat subuh,sudah sholat dhuha,sudah murojaah quran?mudah mudahan semua menjalankan perintah Allah amiin.Hari ini kita belajar matematika tentang bangun ruang sisi lengkung.Silahkan pelajari dan kerjakan tugasnya latihan soal di bawah kirim ke WA:082280107255 jangan lupa kirimkan foto belajarnya.dan berikan komentar melalui blogger dan simaskot.Selamat belajar semoga sukses.

D.MATERI

Pengertian Tabung

Tabung adalah sebuah bangun ruang 3 dimensi yang dibentuk oleh 2 buah lingkaran identik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut.

Ciri-ciri Tabung

Sebuah tabung memiliki ciri-ciri sebagai berikut:

• Mempunyai 2 rusuk
• Alas dan tutup berbentuk lingkaran
• Mempunyai 3 bidang sisi (bidang alas, bidang selimut, bidang penutup/atap)

Unsur-unsur Tabung

Unsur-unsur pembentuk sebuah tabung adalah:

Alas dan atap

Alas dan atap sebuah tabung adalah bagian berbentuk lingkaran yang berada di bawah (alas) dan atas (atap).

Selimut tabung

Selimut tabung adalah sebuah sisi lengkung yang menghubungkan sisi alas dengan sisi atap.

Rusuk tabung

Rusuk tabung adalah sisi alas / atap yang berbentuk lingkaran dan merupakan perpotongan antara alas / atap dengan selimut tabung.

Rumus Tabung

Rumus Luas Permukaan Tabung

Luas permukaan tabung dapat dihitung dengan menjumlahkan luas ketiga sisinya, yaitu

Luas Permukaan Tabung = Luas Alas + Luas Atap + Luas Selimut Tabung

Luas alas = luas atap = π × r²

Luas selimut tabung = 2 × π × r × t

Jadi Luas Permukaan tabung adalah

L = π × r² + π × r² + 2 × π × r × t

L = 2 × π × r² + 2 × π × r × t

L = 2 π r (r + t)

Keterangan :

• L = Luas permukaan tabung
• π =phi (22/7 atau 3,14)
• r =jari – jari alas / atap
• t =tinggi tabung

Rumus Volume Tabung

Volume tabung dapat dihitung dengan rumus berikut:

V = Luas alas × tinggi

V = π × r² × t

V = π r² t

Keterangan:

• V = Volume tabung
• π =phi (22/7 atau 3,14)
• r =jari – jari alas / atap
• t =tinggi tabung

Contoh Soal Tabung

Berikut adalah contoh soal tabung lengkap dengan pembahasan jawabannya:

Contoh 1

Sebuah tabung memiliki jari – jari 14 cm dan tinggi 10 cm, hitunglah luas permukaan dan volume dari tabung tersebut?

Penyelesaian:

L = 2 π r (r + t)

L = 2 × 22/7 × 14cm × (14cm + 10cm)

L = 2 × 22 × 2cm × 24cm

L = 2.112cm²

V = π r² t

V = 22/7 × (14cm)² × 10cm

V = 6.160cm³

Jadi luas permukaan dan volume tabung tersebut masing-masing adalah 2.112cm² dan 6.160cm³.

Contoh 2

Diketahui sebuah tabung memiliki luas permukaan 616cm² . Jika jari-jari tabung tersebut adalah 7cm, maka hitunglah volume tabung tersebut.

Penyelesaian:

L = 2 π r (r + t)

616cm² = 2 × 22/7 × 7cm × (7cm + t)

616cm² = 44cm × (7cm + t cm)

616cm² = 308cm² + 44cm × t

44cm × t = 616cm² – 308cm² = 308cm² 

t = 308cm² ÷ 44cm

t = 7cm

V = π r² t

V = 22/7 × (7cm)² × 7cm

V = 1.078cm³

Jadi volume tabung tersebut adalah 1.078cm³.

E.SKENARIO/PETUNJUK PEMBELAJARAN

 Pahami materi di atas dan kerjakan di buku latihan soal berikut di kirim ke WA:082280107255 paling lambat senin tanggal 1 maret 2021 pukul 21.00 .Jika tidak mengumpul nilai raport diisi apa adanya tidak akan di bantu nilainya .Jika ada kesulitan mohon di tanyakan pada saat ada jam belajar.Selamat belajar semoga sukses. 

F.LATIHAN SOAL

 1.Sebuah tabung memiliki jari – jari 21 cm dan tinggi 20 cm, hitunglah luas permukaan dan volume dari tabung tersebut?

Penyelesaian:

 2.Diketahui sebuah tabung memiliki luas permukaan 596,6 cm² . Jika jari-jari tabung tersebut adalah 5cm, maka hitunglah volume tabung tersebut.

Penyelesaian:

KELILING DAN LUAS LINGKARAN

 

 HARI/TANGGAL:SELASA/23 FEBRUARI 2021

MATA PELAJARAN:MATEMATIKA

KELAS                  :8D,8E,8F,8G

A.KOMPETENSI DASAR

 4.7 Menyelesaikan masalah yang berkaitan dengan sudut pusat, sudut keliling, panjang busur, dan luas juring lingkaran, serta hubungannya

B.TUJUAN PEMBELAJARAN

 Siswa diharapkan dapat : 

 Menyajikan hasil pembelajaran tentang lingkaran

Menyelesaikan masalah yang berkaitan dengan lingkaran

C.APERSEPSI

Assalamualaikum wr.wb anak-anak soleh-solehah bagaimana khabarnya hari ini sudsh sholat subuh,sudah sholat dhuha,sudah murojaah quran?mudah mudahan semua menjalankan perintah Allah amiin.Hari ini kita belajar matematika tentang Luas dan Keliling lingkaran .Silahkan pelajari dan kerjakan tugasnya kirim ke WA:082280107255 jangan lupa kirimkan foto belajarnya.dan berikan komentar melalui blogger dan simaskot.Selamat belajar semoga sukses. 

D.MATERI

Rumus Luas Lingkaran

 

Luas lingkaran bisa dihitung menggunakan rumus:

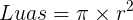
Keterangan:

π = phi = 3,14 atau 22/7

r = jari-jari, (satuan yang digunakan tergantung dari soal yang dibrikan, bisa cm, dm ataupun m, dan satuan luas adalah kuadrat atau persegi, misal cm² atau m²)

Contoh Soal dan Pembahasan Luas Lingkaran

1. jika diketahui sebuah lingkaran mempunyai diameter 28 cm. Berapakah luas lingkaran tersebut?

Penyelesaian:

Diketahui:

d = 28 cm

d = 2 x r

r = d/2

r = 28/2

r = 14 cm

Ditanyakan: Luas lingkaran?

Jawab:

Luas = π × r²

Luas = 22/7 × 14²

  = 22/7 x 196

  = 22 x 28 = 616 cm²

Jadi, luas lingkaran tersebut adalah 616 cm².

2. Sebuah lingkaran memiliki jari-jari sebesar 20 cm. Berapakah luas lingkaran tersebut?

Penyelesaian:

Diketahui:

r = 20 cm

Ditanyakan: Luas lingkaran?

Jawab:

Luas = π × r²

  = 3,14 × 200

  = 628 cm²

Jadi, luas lingkaran tersebut adalah 628 cm²

Rumus Keliling Lingkaran dengan Jari-Jari

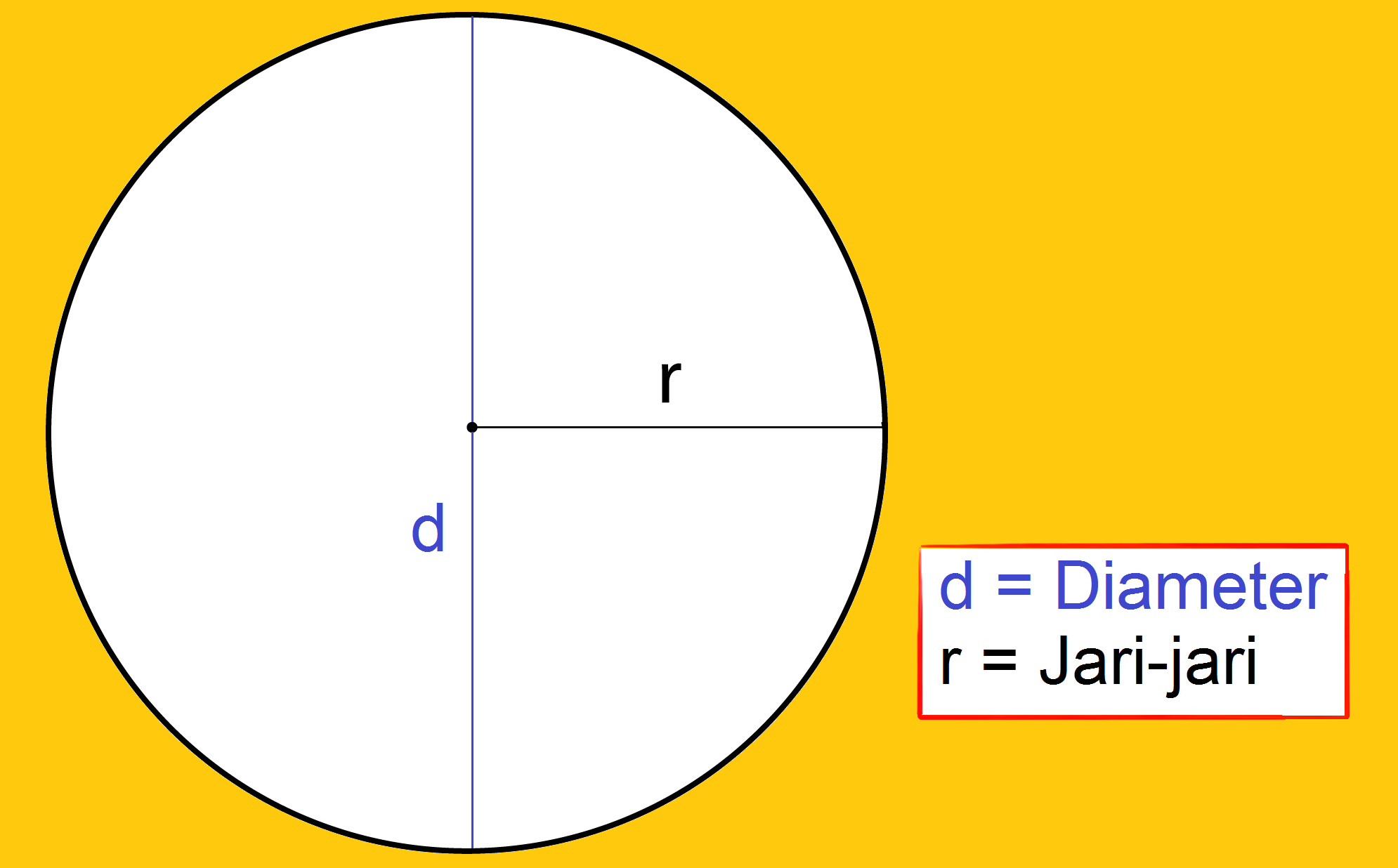
Saat mencari keliling lingkaran, maka ada dua rumus yang bisa di gunakan. Rumus pertama digunakan jika lingkaran tersebut diketahui diameternya. Dan rumus kedua digunakan untuk menghitung keliling lingkaran yang belum diketahui diameternya. Berikut adalah pembahasan beserta contohnya.

Jika diameternya tidak diketahui maka kita bisa menggunakan jari-jari untuk menghitung keliling lingkaran. Rumus yang digunakan adalah:

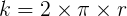
Keterangan:

k = Keliling lingkaran

π = phi; nilainya 22/7 atau3,14

r = jari-jari lingkaran

Contoh Soal dan Pembahasan

Supaya lebih memahami cara menghitung keliling lingkaran maka berikut adalah contoh soal beserta pembahasannya:

1. Ada sebuah lingkaran dengan jari-jari 50 cm, berapakah keliling lingkaran tersebut?

Jawaban:

Diketahui:

r = 50 cm

π = 22/7 atau 3,14

Maka,

k = 2 x π x r

  = 2 x 3,14 x 50

  = 314 cm

Jadi keliling lingkaran tersebut adalah 314 cm.

2. Ada sebuah lingkaran dengan jari-jari 49 cm, berapakah keliling lingkaran tersebut?

Jawaban:

Diketahui:

r = 49 cm

π = 22/7 atau 3,14

Maka,

k = 2 x π x r

   = 2 x 22/7 x 49

   = 2 x 22 x 7 = 308 cm

Jadi keliling lingkaran tersebut adalah 308 cm.

Rumus Keliling Lingkaran Dengan Diameter

Rumus ini berlaku jika yang diketahui adalah diameter lingkarannya. Untuk menghitung keliling suatu lingkaran menggunakan diameter, gunakan rumus berikut:

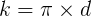
Keterangan:

k = keliling lingkaran

π = phi =22/7 atau 3,14

d = diameter

Contoh Soal dan Pembahasan

1. Berapa keliling lingkaran jika diameternya 30 cm?

Jawaban:

Keliling = π x d

= 3,14 x 30

= 94,2 cm

Jadi keliling lingkaran tersebut adalah 94,2 cm

2. Berapa keliling lingkaran jika diameternya 105 cm?

Jawaban:

Keliling = π x d

= 22/7 x 105

= 330 cm

Jadi keliling lingkaran tersebut adalah 330 cm.

Rumus Diameter Lingkaran

Jika yang diketahui adalah keliling dari lingkarannya maka rumus yang digunakan adalah rumus diameter lingkaran seperti di bawah ini:

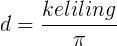
Keterangan:

d = diameter

π = phi, nilainya 22/7 atau 3,14

Keliling = keliling lingkaran yang sudah ada

Contoh Soal dan Pembahasan

Berikut adalah contoh soal dan pembahasan dari diameter lingkaran:

1. Ada sebuah papan berbentuk lingkaran dengan keliling 95 cm. Berapakah diameternya?

Jawaban:

Diketahui:

Keliling = 95 cm

Diameter?

Rumus keliling = π x d

Jika yang diketahui adalah kelilingnya, makan gunakan rumus berikut:

d = keliling / π

Maka,

d = 95/3,14 = 30, 25 cm

Jadi, diameter lingkaran tersebut adalah 24,5 cm

2. Diketahui sebuah lingkaran memiliki keliling sebesar 66 cm. Hitunglah berapa diameter lingkaran tersebut.

Jawaban:

Diketahui:

Keliling = 66 cm

Ditanyakan: Diameter lingkaran?

Jawab:

Keliling = π × d

Maka,

d = keliling / π

    = 66 / (22/7)

    = (66 × 7) / 22 = 21 cm

Jadi, diameter lingkaran tersebut adalah 21 cm.

Hitunglah jari-jari dan diameter lingkaran yang mempunyai luas 200,96 cm² !

Diketahui:

L = 200,96 cm²

Ditanya:

Jari-jari dan diameter lingkaran!

Penyelesaian:

• Mencari jari-jari Lingkaran (r)

   

Mencari Diameter Lingkaran (d)

• Karena nilai r  = 8 cm, sehingga diperoleh d = 2 × 8 cm = 16 cm

Jadi, jari-jari lingkaran tersebut adalah 8 cm.
Jadi, diameter lingkaran tersebut adalah 16 cm.

 D. SKENARIO/PETUNJUK PEMBELAJARAN

 Pahami materi di atas dan kerjakan di buku latihan soal berikut di kirim ke WA:082280107255 paling lambat selasa tanggal 23 februari 2021 pukul 21.00 .Jika tidak mengumpul nilai raport diisi apa adanya tidak akan di bantu nilainya .Jika ada kesulitan mohon di tanyakan pada saat ada jam belajar.Selamat belajar semoga sukses. 

 

E.LATIHAN SOAL

 

Soal Nomor 1
Sebuah hiasan dibuat berbentuk seperti setengah lingkaran.

Keliling hiasan itu adalah $\cdots \cdot$
A. $88\text{cm}$                         C. $144\text{cm}$
B. $116\text{cm}$                       D. $176\text{cm}$

Pembahasan

Soal Nomor 2
Sebuah jam dinding yang berbentuk lingkaran memiliki panjang diameter $28\text{cm}$

. Keliling jam dinding tersebut adalah $\cdots \cdot (\pi =\frac{22}{7})$
A. $86\text{cm}$                         C. $90\text{cm}$
B. $88\text{cm}$                         D. $92\text{cm}$

Pembahasan

Soal Nomor 3
Nathan memiliki hula hoop dengan keliling $220$

cm. Panjang jari-jari hula hoop itu adalah $\cdots \cdot (\pi =\frac{22}{7})$
A. $28\text{cm}$                            C. $35\text{cm}$
B. $30\text{cm}$                            D. $42\text{cm}$

Pembahasan

Soal Nomor 4
Ibu membuat taplak meja berbentuk lingkaran berdiameter $1,4\text{m}$

. Setelah selesai dibuat, ibu mengukur keliling taplak mejanya. Kelilingnya adalah $\cdots \cdot (\pi =\frac{22}{7})$
A. $3,75\text{m}$                          C. $4,20\text{m}$
B. $4,00\text{m}$                          D. $4,40\text{m}$

Pembahasan

Soal Nomor 5
Sebuah lapangan berbentuk lingkaran berdiameter $60\text{m}$

. Sukardi berlari mengelilingi lapangan tersebut sebanyak $3$ kali. Jarak yang ditempuhnya adalah $\cdots \cdot (\pi =3,14)$
A. $562,5\text{m}$                       C. $565,5\text{m}$
B. $565,2\text{m}$                       D. $565,8\text{m}$

Pembahasan

6..Sebuah lingkaran memiliki jari-jai 20 cm tentukan luas lingkaran tersebut.

a.1056 cm²
b.1156 cm²
c.1256 cm²
d.1356 cm²

Pembahasan : soal di atas adalah soal untuk mencari luas lingakran yang jari-jarinya adalah 20 cm. Maka sebagai berikut :
πr² => 3,14(20)² = > 

7..Perhatikan gambar lingkaran dibawah ini :

Luas gambar lingkran di atas adalah…

a.149,72 cm²
b.150,72 cm²
c.151,72 cm²
d.152,72 cm²

Pembahasan : soal di atas adalah soal untuk mengetahui luas dari gambar lingkaran dengan diameter 12 di atas maka cara mengerjakan adalah dengan rumus 1/4πd² => 1/4 (3,14)(12)² => 

8.Sebua lingkaran memiliki jari 28 cm seperti gambar di sampin. Maka luas dari lingkara disamping adalah

a.2261,76 cm²
b.2361,76 cm²
c.2461,76 cm²
d.2561,76 cm²

Pembahasan : soal lingkaran di samping adalah soal tentang luas lingkaran. Maka untuk mengerjakannya adalah dengan menggunakan rumus lingkaran sperti berikut : πr² => 3,14(28)² = > 

9..Perhatikan gambar disamping, jika luas lingkaran disamping adalah 452,16² cm maka jari-jarinya adalah

a. 2,46 cm

b.3,46 cm

c. 4,46 cm

d. 5,46 cm

 Pembahasan : soal di atas adalah soal tentang menari jari-jari dari luas ligkaran yang ada pada gambar di samping maka sebagai berikut : luas = πr² => r² = luas/π = 452,16/3,14 = 

 10..Perhatikan gambar dibawah ini :

Gambar di atas adalah 1/2 dari lingkaran jika jari-jarinya adalah 7 maka tentukan luas gambar tersebbut :a.73,93 cm² 

b.74,93 cm²
c.75,93 cm²
d.76,93 cm²

Pembahasan : gambar tersebut adalah gambar seperempat lingkaran maka untuk mencarinya kita bisa membuat rumus : πr² maka jika 1/2 sama dengan 1/2 πr² =

11.Sebuah lingkaran memiliki diameter 14 cm tentukan luas dari lingkaran tersebut!

a.151,86 cm²
b.152,86 cm²
c.153,86 cm²
d.154,86 cm²

Pembahasan : soal di atas adalah soal untuk mencari luas lingkaran meggunakan diameter lingkaran maka untuk mengerjakannya adalah meggunakan cara ke dua lingkaran seperti berikut :
1/4πr² =

12.Jika luas lingkaran adalah 96 cm² maka jari-jari dari lingkaran tersebut adalah..

a.3,18 cm
b.3,28 cm
c.3,38 cm
d.3,48 cm

Pembahasan : soal nomer 9 sama dengan soal nomor 6 yaitu soal mencari jari-jari lingkaran yag telah diketahui luasnya maka untuk mengerjakannya kita bisa menggunakan cara lingkaran :
πr² = r²= luas/π = 96/3,14 =

14.Perhatikan gambar lingkaran dibawah ini :

Keliling lingkaran di atas adalah 44 cm maka luas dari lingkaran tersebut :

a.144 cm²
b.154 cm²
c.164 cm²
d.174 cm²

Pembahasan : soal di atas soal untuk mencari luas lingkaran ag tela diketehui kelilingnya maka untuk mengerjakannya adalah sebagai berikut :
Keliling = 2πr maka untuk mencari luas lingkaran kita kan mencari jari-jari lingkaran dalam lingkaran maka sebagai berikut :

Jari-jari lingkaran adalah 7 cm maka luas lingkaran tersebut adalah sebagai berikut 

15.Sebuah benda berbentuk dengan lingkaran seperti gambar di bawah :

a.2,74 cm.
b.3,74 cm.
c.4,74 cm.
d.5,74 cm.

Jika luas benda di atas adalah 42 cm² maka jari-jari dari lingkaran terebut adalah

Pembahasan :
Soal di atas adalah soal jari-jari lingkaran mencari jika diketahui luas lingkaran di atas. Maka untuk mencarinya adalah kita meggunakan rumus luas lingkaran maka untuk mengerjakannya adalah sebagai berikut :

Maka jawaban yang tepat adalah