SEGITIGA SEBANGUN PADA SEGITIGA GARIS SEJAJAR

 HARI/TANGGAL:SENIN/15 FEBRUARI 2021

MATA PELAJARAN:MATEMATIKA

KELAS                  :9A

A.KOMPETENSI DASAR

 3.6 Menjelaskan dan menentukan kesebangunan dan kekongruenan antar bangun datar

4.6 Menyelesaikan masalah yang berkaitan dengan kesebangunan dan kekongruenan antar bangun datar

B.TUJUAN PEMBELAJARAN

 Siswa diharapkan dapat :

 Menyelesaikan masalah yang Menyajikan hasil pembelajaran tentang kesebangunan dan kekongruenan

  Menyelesaikan masalah yang berkaitan dengan kesebangunan dan kekongruenan

C.APERSEPSI

Assalamualaikum wr.wb anak-anak soleh-solehah bagaimana khabarnya hari ini sudah sholat subuh,sudah sholat dhuha,sudah murojaah quran?mudah mudahan semua menjalankan perintah Allah amiin.Hari ini kita belajar matematika tentang Kesebangunan dan Kekongruenan Segitiga sebangun pada segitiga garis sejajar.Silahkan pelajari dan kerjakan tugasnya latihan soal di bawah kirim ke WA:082280107255 jangan lupa kirimkan foto belajarnya.dan berikan komentar melalui blogger dan simaskot.Selamat belajar semoga sukses.

D.MATERI

Perbandingan Ruas Garis Sejajar pada Segitiga

Perhatikan segitiga di bawah ini.

Pada segitiga tersebut, sisi f yang sejajar dengan e, sehingga diperoleh:

cc+d=aa+b=ef

cd=ab

Perbandingan Ruas Garis pada Segitiga Terpancung (Trapesium)

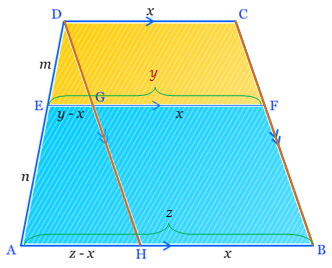
Perhatikan gambar di bawah ini.

Oleh karena garis EG sejajar dengan garis AH, maka segitiga ΔDEG sebangun dengan segitiga ΔDAH, sehingga berlaku:

DEDA=EGAH

⇔mm+n=y−xz−x

⇔m(z−x)=(m+n)(y−x)

⇔mz−mx=my−mx+ny−nx

⇔mz=my+ny−mx+mx−nx

⇔mz=(m+n)y−nx

⇔(m+n)y=mz+nx

⇔y=mz+nxm+n

Dengan demikian, pada segitiga terpancung (trapesium) ABCD berlaku:

y=mz+nxm+n

Contoh 1

Perhatikan gambar berikut.

Jika panjang AB = 3 cm, BC = 2 cm, dan DE = 3 cm, maka tentukan panjang BD.

Penyelesaian:

Diketahui:
panjang AB = 3 cm
panjang BC = 2 cm
panjang DE = 3 cm

Misalkan panjang BD = p.

Panjang BD dapat ditentukan dengan perbandingan ruas garis sejajar pada segitiga.

Pada segitiga tersebut, sisi DE yang sejajar dengan BC, sehingga diperoleh dua buahsegitiga yang sebangun yaitu ΔADE dan ΔABC.

Ini berarti, salah satu perbandingan sisi bersesuaiannya adalah:

ADAB=DEBC⇔(3+p)3=32⇔2(3+p)=3(3)⇔6+2p=9⇔2p=9–6⇔2p=3⇔p=1,5

Jadi, panjang BD = p = 1,5 cm.

Contoh 2

Perhatikan gambar berikut.

Diketahui ΔACB siku-siku di C. Jika panjang AD = 32 cm dan DB = 8 cm, maka tentukan panjang CD.

Penyelesaian:

Untuk menentukan panjang CD, gunakan perbandingan ruas garis pada segitiga siku-siku.

Berdasarkan gambar pada soal diperoleh ΔADC sebangun dengan ΔCBD, sehingga salah satu perbandingan sisi bersesuaiannya adalah:

ADCD=CDBD⇔CD2=AD×BD⇔CD2=32×8⇔CD2=256−−−√⇔CD=16

Jadi, panjang CD = 16 cm.

Contoh 3

Perhatikan gambar di bawah ini.

Diketahui panjang AB = 15 cm, DC = 9 cm, dan AE : ED = 2 : 1. Tentukan panjang EF.

Penyelesaian:

Panjang EF dapat ditentukan dengan perbandingan ruas garis pada segitiga terpancung (trapesium).

Ini berarti:
panjang m = nilai perbandingan ED = 1
panjang n = nilai perbandingan EA = 2
panjang z = panjang AB = 15 cm
panjang x = panjang DC = 9 cm

y=mz+nxm+n

⇔EF=ED.AB+EA.DCED+EA⇔EF=15(1)+9(2)1+2⇔EF=15+183⇔EF=333⇔EF=11

Jadi, panjang sisi EF adalah 11 cm.

E.SKENARIO/PETUNJUK PEMBELAJARAN

 Pahami materi di atas dan kerjakan di buku latihan soal berikut di kirim ke WA:082280107255 paling lambat senin tanggal 15 februari 2021 pukul 21.00 .Jika tidak mengumpul nilai raport diisi apa adanya tidak akan di bantu nilainya .Jika ada kesulitan mohon di tanyakan pada saat ada jam belajar.Selamat belajar semoga sukses. 

F.LATIHAN SOAL

1.Perhatikan gambar berikut.

Jika panjang AB = 6 cm, BC = 4 cm, dan DE = 6 cm, maka tentukan panjang BD

2.Perhatikan gambar berikut.

Diketahui ΔACB siku-siku di C. Jika panjang AD = 32 cm dan DB = 8 cm, maka tentukan panjang CD.

 

3.Perhatikan gambar di bawah ini.

Diketahui panjang AB = 30 cm, DC = 18 cm, dan AE : ED = 2 : 1. Tentukan panjang EF.