GARIS SINGGUNG LINGKARAN

 

HARI/TANGGAL:SELASA/30 MARET 2021

MATA PELAJARAN:MATEMATIKA

KELAS                  :8D,8E,8F,8G

A. KOMPETENSI DASAR

4.8 Menyelesaikan masalah yang berkaitan dengan garis singgung persekutuan luar dan persekutuan dalam dua lingkaran

 B. INDIKATOR

·       Menyajikan hasil pembelajaran tentang garis singgung lingkaran

Menyelesaikan masalah yang berkaitan dengan garis singgung lingkaran

C. TUJUAN PEMBELAJARAN 

Siswa diharapkan dapat :

·       Menyajikan hasil pembelajaran tentang garis singgung lingkaran

Menyelesaikan masalah yang berkaitan dengan garis singgung lingkaran

D..APERSEPSI

Assalamualaikum wr.wb anak-anak soleh-solehah bagaimana khabarnya hari ini sudsh sholat subuh,sudah sholat dhuha,sudah murojaah quran?mudah mudahan semua menjalankan perintah Allah amiin.Hari ini kita belajar matematika Garis singgung lingkaran .Silahkan pelajari dan kerjakan tugasnya kirim ke WA:082280107255 jangan lupa kirimkan foto belajarnya.dan berikan komentar melalui blogger dan simaskot.Selamat belajar semoga sukses. 

E.MATERI

Pengertian Garis Singgung Lingkaran

Pengertian garis singgung lingkaran yaitu suatu garis yang memotong lingkaran hanya pada satu titik dan garis tersebut tegak lurus terhadap garis tengah atau diameter lingkaran atau jari jari yang di tarik melalui titik singgung.

 

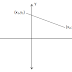
Perhatikan gambar di atas,  Garis yang telihat dalam gambar menyinggung atau memotong lingkaran di titik A. Dan bila di tarik garis dari titik O pusat lingkaran menuju titik singgung yaitu titik A akan membentuk sebuah garis tegak lurus. Seperti itulah yang disebut garis singgung lingkaran.()

Sifat sifat Garis Singgung Lingkaran

Garis singgung lingkaran mempunyai beberapa sifat yang tercipta dari definisi garis singgung itu sendiri. Sifat-sifatnya adalah :
 

• Setiap garis singgung lingkaran tegak lurus terhadap diameter lingkaran yang ditarik melalui titik singgungnya. Titik singgung adalah titik pertemuan dari garis singgung dan lingkaran.

• Melalui titik pada lingkaran hanya dapat dilakukan sekali dan hanya satu garis yang bersinggungan dengan lingkaran.
• Melalui sebuah titik luar lingkaran dapat dibuat dua garis yang bersinggungan dengan lingkaran.
• Jika dua garis singgung berpotongan pada suatu titik di luar lingkaran, maka jarak antara titik persimpangan itu sama dengan titik-titik singgung 

A. Menentukan Panjang Garis Singgung yang Melalui Satu Titik Di Luar Lingkaran

Lingkaran berpusat di titik O dengan jari-jari OA dan OA tegak lurus garis PA. Garis PA adalah garis singgung lingkaran melalui titik P di luar lingkaran. Karena setiap sudut yang dibentuk oleh garis yang melalui titik pusat dan garis singgung lingkaran besarnya 90^o maka segitiga PAO adalah segitiga siku-siku PAO. Dengan teorema Pythagoras berlaku

Sehingga, panjang garis singgung lingkaran (PA) dapat dicari dengan menggunakan rumus

 

Contoh:
Diketahui lingkaran berpusat di titik O dengan jari-jari OB = 3 cm. Garis AB adalah garis singgung lingkaran yang melalui titik A di luar lingkaran. Jika jarak OA = 5 cm maka tentukan panjang garis singgung AB.

Jawab:

Jadi, panjang garis singgung AB = 4 cm

B. Menentukan  Panjang Garis Singgung Persekutuan Dalam Dua Lingkaran

 

Dari gambar tersebut diperoleh
jari-jari lingkaran yang berpusat di M = R;
jari-jari lingkaran yang berpusat di N = r;
panjang garis singgung persekutuan dalam adalah AB = d;
jarak titik pusat kedua lingkaran adalah MN = p.
Jika garis AB digeser sejajar ke atas sejauh BN maka diperoleh garis ON.
Garis ON sejajar AB, sehingga sudut MON = sudut MAB = 90^o (sehadap).
Perhatikan segi empat ABQS.
Garis AB//SQ, AS//BQ, dan sudut PSQ = sudut PAB = 90^o.

Jadi, segi empat ABNO merupakan persegi panjang dengan panjang AB = d dan lebar BN = r. Perhatikan bahwa segitiga MNO siku-siku di titik O. Dengan menggunakan teorema Pythagoras diperoleh

 

Karena panjang ON = AB dan MO = R + r, maka rumus panjang garis singgung persekutuan dalam dua lingkaran (d) dengan jarak kedua titik pusat p, jari-jari lingkaran besar R, dan jari-jari lingkaran kecil r adalah

 

Contoh:

Panjang jari-jari dua lingkaran masing-masing adalah 4 cm dan 3 cm. Jarak kedua titik pusatnya adalah 25 cm. Hitunglah panjang garis singgung persekutuan dalam kedua lingkaran tersebut!

Jawab:

 

Jadi, panjang garis singgung persekutuan dalam kedua lingkaran = 24 cm

C. Menentukan Panjang Garis Singgung Persekutuan Luar Dua Lingkaran

Dari gambar tersebut diperoleh
jari-jari lingkaran yang berpusat di M = R;
jari-jari lingkaran yang berpusat di N = r
panjang garis singgung persekutuan luar adalah AB = l;
jarak titik pusat kedua lingkaran adalah MN = p.
Jika garis AB kita geser sejajar ke bawah sejauh BN maka diperoleh garis ON.
Garis AB sejajar ON, sehingga sudut MON = sudut MAB = 90^o (sehadap).
Perhatikan segi empat ABQS. Garis AB//SQ, AS//BQ, dan sudut PSQ = sudut PAB = 90^o.
Segitiga MNO  siku-siku di O, sehingga berlaku

 

Karena panjang ON = AB dan MO = R - r, maka rumus panjang garis singgung persekutuan luar dua lingkaran (l) dengan jarak kedua titik pusat p, jari-jari lingkaran besar R, dan jari-jari lingkaran kecil r adalah

Contoh:
Panjang jari-jari dua lingkaran masing-masing adalah 15 cm dan 5 cm. Panjang garis singgung persekutuan luar kedua lingkaran adalah 24 cm. Hitunglah jarak kedua titik pusat kedua lingkaran tersebut!
Jawab:
 
Jadi, jarak kedua titik pusatnya = 26 cm

E. SKENARIO/PETUNJUK PEMBELAJARAN

Pahami materi di atas dan kerjakan di buku latihan soal berikut di kirim ke WA:082280107255 paling lambat selasa tanggal 30 maret 2021 pukul 21.00 .Jika tidak mengumpul nilai raport diisi apa adanya tidak akan di bantu nilainya .Jika ada kesulitan mohon di tanyakan pada saat ada jam belajar.Selamat belajar semoga sukses. 

 F.LATIHAN SOAL

1.Diketahui lingkaran berpusat di titik O dengan jari-jari OB = 6 cm. Garis AB adalah garis singgung lingkaran yang melalui titik A di luar lingkaran. Jika jarak OA = 10 cm maka tentukan panjang garis singgung AB.

2. Panjang jari-jari dua lingkaran masing-masing adalah 2 cm dan 6 cm. Jarak kedua titik pusatnya adalah 17 cm. Hitunglah panjang garis singgung persekutuan dalam kedua lingkaran tersebut!

 3.Panjang jari-jari dua lingkaran masing-masing adalah 8 cm dan 3 cm. Panjang garis singgung persekutuan luar kedua lingkaran adalah 12 cm. Hitunglah jarak kedua titik pusat kedua lingkaran tersebut!

 

 

 

SIMULASI SOAL UNBK 2021

HARI/TANGGAL:SENIN/29 MARET 2021

MATA PELAJARAN:MATEMATIKA

KELAS                  :9A

A.KOMPETENSI DASAR

 3.7 Membuat generalisasi luas permukaan dan volume berbagai bangun ruang sisi lengkung (tabung, kerucut, dan bola)

B.TUJUAN PEMBELAJARAN

 Siswa diharapkan dapat :

 ·      Membuat generalisasi luas permukaan dan volume bangun ruang sisi lengkung tabung

·      Membuat generalisasi luas permukaan dan volume bangun ruang sisi lengkung kerucut

·      Membuat generalisasi luas permukaan dan volume bangun ruang sisi lengkung bola

C.APERSEPSI

Assalamualaikum wr.wb anak-anak soleh-solehah bagaimana khabarnya hari ini sudah sholat subuh,sudah sholat dhuha,sudah murojaah quran?mudah mudahan semua menjalankan perintah Allah amiin.Hari ini kita belajar matematika tentang Soal UNBK.Silahkan pelajari dan kerjakan tugasnya latihan soal di bawah kirim ke WA:082280107255 jangan lupa kirimkan foto belajarnya.dan berikan komentar melalui blogger dan simaskot.Selamat belajar semoga sukses.

SOAL DAN PEMBAHASAN SIMULASI UNBK MATEMATIKA SMP/MTS 2020 (Bagian 1) Nomor 1 - 10 

 SOAL 1.

Urutan kecil ke besar bilangan 62%; 0,6; 0,63; 9/14 adalah ....
A. 0,6; 62%; 0,63; 9/14
B. 0,6; 62%; 9/14; 0,63
C. 0,63; 9/14; 62%; 0,6
D. 9/14; 0,63; 62%; 0,6
Pembahasan:
Pertama kita harus ubah dulu semua pecahan ke dalam bentuk desimal.

62% = 62/100 = 0,62
0,6 = 0,6
0,63 = 0,63
9/14 = 0,64
Dari pecahan-pecahan desimal di atas, maka : 0,6 < 0,62 < 0,63 < 0,64. Sehingga urutanya adalah :
0,6; 62%; 0,63; 9/14. Kunci : A

SOAL 2.
Nilai dari (88–√)−2 adalah ....
A. -1/512
B. 1/512
C. 1/256
D. 512
Pembahasan :
(88–√)−2
= 8−2(812)−2
= 8−28−1
= 8−2+(−1) = 8−3
= 183 = 1512.
Kunci : B

SOAL 3.
Hasil dari 26–√×8–√+412−−√ adalah ....
A. 86–√
B. 123–√
C. 163–√
D. 1215−−√
Pembahasan :
26–√×8–√+412−−√
= 248−−√+412−−√ = 216×3−−−−−√+44×3−−−−√
= 2⋅43–√+4⋅23–√
= 83–√+83–√=163–√
Kunci : C

SOAL 4.
Pada ujian bahasa, skor total ditentukan dengan aturan: skor 4 untuk jawaban benar, skor -2 untuk jawaban salah, dan skor -1 untuk jawaban kosong. Dari 40 soal yang diberikan , seorang peserta tes menjawab 37 soal dan mendapatkan skor 115. Jumlah soal yang dijawab benar oleh peserta tersebut adalah ....
A. 18 soal
B. 19 soal
C. 31 soal
D. 32 soal
Pembahasan :
Karena ada 3 soal yang tidak terjawab, maka total nilai untuk 37 soal (baik benar maupun salah) adalah total nilai 37 soal yang belum dikurangi 3 soal yang tidak terjawab. Sehingga total nilai 37 soal diluar yang tidak terjawab: 115 + 3(1) = 118.
Misalkan jumlah soal yang dijawab benar = a, dan yang dijawab salah = b.
a + b = 37 ... (i)
4a - 2b = 118 ... (ii)
Dengan mengeliminasi b pada persamaan (i) dan (ii) diperoleh a = 32.
Jadi, banyak soal yang dijawab benar = a = 32 soal.
Kunci : D

SOAL 5.
Apabila hari pendidikan nasional pada tanggal 2 Mei adalah hari Selasa, HUT Kemerdekaan RI tanggal 17 Agustus pada tahun yang sama adalah ....
A. hari Rabu
B. hari Kamis
C. hari Sabtu
D. hari Minggu
Pembahasan :
3 Mei – 31 Mei = 29 hari
1 Juni – 30 Juni = 30 hari
1 Juli – 31 Juli = 31 hari
1 Agustus – 17 Agustus = 17 hari
Sehingga total rentang harinya : 29 + 30 + 31 + 17 = 107 hari
Karena 1 minggu ada 7 hari (dari Selasa sampai Selasa minggu depan), maka hari selanjutnya dapat diketahui dari sisa pembagian 107 dibagi 7.
107 dibagi 7 memiliki sisa 2. Maka 2 hari setelah hari Selasa adalah hari Kamis.
Kunci : B

SOAL 6.
Seorang pemborong memperkirakan dapat menyelesaikan suatu pekerjaan dalam 24 hari dengan 7 orang pekerja. Bila pekerjaan itu ingin diselesaikan dalam waktu 14 hari, maka pekerja yang harus disediakan adalah ....
A. 20 orang
B. 18 orang
C. 15 orang
D. 12 orang
Pembahasan :
Kasus ini merupakan perbandingan tak senilai. Misalkan banyak pekerja yang dibutuhkan untuk menyelesaikan pekerjaan selama 14 hari = a, maka persamaannya :
a⋅14aa=7⋅24=7×2414=12
Jadi pekerja yang harus disediakan adalah 12 pekerja.
Kunci : D

SOAL 7.
Diketahui K=65L dan L=79M. Perbandingan K, L, dan M adalah ....
A. 42 : 35 : 45
B. 42 : 45 : 35
C. 45 : 42 : 54
D. 45 : 54 : 42
Pembahasan :
Perhatikan L=79M→M=97L.
Maka K : L : M sebagai berikut :
K:L:M=65L:L:97L.
Agar penyebut 5 dan 7 dapat disederhanakan, pilih L = 35, maka :
65(35):(35):97(35)
= 42:35:45
Jadi perbandingan K, L, dan M adalah 42 : 35 : 45.
Kunci : A

SOAL 8.
Ruangan berukuran 60 m x 75 m. Denah ruangan tersebut akan dibuat dengan ukuran 80 cm x 100 cm. Skala untuk menggambar denah adalah ....
A. 1 : 100
B. 1 : 75
C. 1 : 60
D. 1 : 50
Pembahasan :
Ambil salah satu sampel yang bersesuaian. Misal kita ambil yang 60 m pada ukuran sebenarnya dan 80 cm ukuran denah. Maka skalanya adalah :
80cm60m=80cm6000cm=175.
Jadi skala yang digunakan adalah 1 : 75.
Kunci : B

SOAL 9.
Rumus suku ke-n suatu barisan dinyatakan dengan Un = 4n + 13. Hasil dari U23+U25 adalah .... A. 244 B. 218 C. 113 D. 105 Pembahasan :
Diketahui Un=4n+13, Maka :
U23=4(23)+13=92+13=105
U25=4(25)+13=100+13=113
Maka : U23+U25= 105 + 113 = 218
Kunci: B

SOAL 10.
Ibu Eti menabung di Bank sebesar Rp3.500.000,00, dengan suku bunga tunggal sebesar 12% per tahun. Saat diambil, jumlah tabungan Ibu Eti menjadi Rp3.815.000,00. Lama Ibu Eti menabung adalah ....
A. 9 bulan
B. 8 bulan
C. 7 bulan
D. 6 bulan
Pembahasan :
Besar bunga selama n bulan = 3.815.000 - 3.500.000 = 315.000 n12×x100×Mn12×12100×3.500.000n×35.000nn=bunga n bulan=315.000=315.000=315.00035.000=9
Jadi lama Ibu Eti menabung adalah 9 bulan.
Kunci: A

 Pahami materi di atas dan kerjakan di buku latihan soal berikut di kirim ke WA:082280107255 paling lambat senin tanggal 29 maret 2021 pukul 21.00 .Jika tidak mengumpul nilai raport diisi apa adanya tidak akan di bantu nilainya .Jika ada kesulitan mohon di tanyakan pada saat ada jam belajar.Selamat belajar semoga sukses. 

F.LATIHAN SOAL

 1. Jika bilangan 0,65; $\frac{5}{8}$; 0,7; 69% diurutkan dari yang terkecil maka hasilnya adalah...
0,65; 0,7; $\frac{5}{8}$; 69%
0,65; 69%; $\frac{5}{8}$; 0,7
$\frac{5}{8}$; 0,65; 69%; 0,7
$\frac{5}{8}$; 0,7; 0,65; 69%

2. Hasil dari ${\left(2\sqrt{2}\right)}^{-2}$ adalah...
$\frac{1}{16}$
$\frac{1}{8}$
$\frac{1}{4}$
$\frac{1}{2}$

3. Hasil dari $3\sqrt{6}\times 2\sqrt{2}+4\sqrt{3}$ adalah...
$15\sqrt{3}$
$16\sqrt{3}$
$28\sqrt{3}$
$50\sqrt{3}$

4. Pada tes kemampuan matematika, skor total ditentukan dengan aturan: skor 4 untuk jawaban benar, skor -2 untuk jawaban salah, dan skor -1 untuk soal tidak dijawab. Dari 50 soal yang diberikan, Amir hanya menjawab 48 soal dan memperoleh skor 100. Banyak soal yang dijawab Amir dengan benar adalah...
25 soal
33 soal
40 soal
48 soal

5. Apabila Hari Pendidikan Nasional pada tanggal 2 Mei adalah hari Selasa, HUT kemerdekaan RI pada tanggal 17 Agustus pada tahun yang sama adalah...
hari Rabu
hari Kamis
hari Sabtu
hari Minggu

6. Seorang pemborong dapat menyelesaikan suatu pekerjaan dalam waktu 40 hari dengan 15 pekerja. Jika pekerjaan ingin diselesaikan dalam waktu 30 hari, maka banyak tambahan pekerja yang diperlukan adalah...
5 orang
10 orang
15 orang
20 orang

7. Perbandingan permen Aurel, Rani dan Dhea 5 : 3 : 2. Sedangkan jumlah permen Aurel dan Rani 64. Jumlah permen tiga orang tersebut adalah...
72
80
88
108

8. Suatu gedung perkantoran dengan ukuran 20 meter x 30 meter. Ukuran gedung tersebut pada denah adalah 40 cm x 60 cm. Skala pada denah tersebut adalah...
1 : 50
1 : 100
1 : 500
1 : 1000

9. Rumus suku ke-n barisan adalah $U_n=3n+2$. Jumlah suku ke-25 dan suku ke-27 dari barisan tersebut adalah...
154
160
164
166

10. Ani menabung sebesar Rp. 800.000,00 pada suatu bank yang memberikan suku bunga tunggal sebesar 16% pertahun. Pada saat diambil, tabungan Ani menjadi Rp. 992.000,00. Lama Ani menabung adalah...
8 bulan
18 bulan
24 bulan
32 bulan