Hari,tanggal:Selasa,27 Agustus 2019
Kelas:8D-8G

Cara Menggambar Grafik Fungsi Aljabar pada Bidang Kartesius, Menentukan Titik Potong, Daerah Asal Nilai Fungsi, Interval Fungsi Naik dan Turun, Titik Stasioner Belok - Di Kelas X, Anda telah mempelajari bagaimana menggambar grafik fungsi y = ax² + bx +c dengan langkah-langkah sebagai berikut.

1. Menentukan titik potong grafik y = ax² + bx +c dengan sumbu-x.
2. Menentukan titik potong grafik y = ax² + bx +c dengan sumbu-y.
3. Menentukan koordinat titik balik fungsi.
4. Menentukan persamaan sumbu simetri fungsi.

Contoh Soal 1 :

Buatlah sketsa grafik fungsi f(x) = x³ + 3x²

Pembahasan :

Langkah 1: Menganalisis f(x)

a. Fungsi f(x) = x³ + 3x² terdefinisi untuk semua bilangan real.

Jadi, daerah asal f(x) adalah {x | x ϵ R}.

b. Daerah nilai f(x) = {f(x) | f(x) ϵ R}.

c. Titik potong dengan sumbu koordinat.

• Titik potong dengan sumbu-y.

Titik potong dengan sumbu-y diperoleh untuk x = 0

f(x) = x³ + 3x²

f(0) = 0

Fungsi f(x) memotong sumbu-y di y = 0.

• Titik potong dengan sumbu-x.

Titik potong dengan sumbu-x diperoleh untuk y = 0.

f(x) = x³ + 3x²

y = f(x)

x³ + 3x² = 0

x² (x + 3) = 0

x = 0 atau x = –3

Fungsi f(x) memotong sumbu-x di x = 0 atau x = –3.

Langkah 2: Menganalisis f '(x)

f(x) = x³ + 3x²

f '(x) = 3x² + 6x

a. Titik stasioner diperoleh untuk f '(x) = 0.

f '(x) = 0 ↔ 3x² + 6x = 0

↔ 3x (x + 2) = 0 ↔ x = 0 atau x = –2

Titik stasioner diperoleh dengan menyubstitusikan x = 0 dan x = –2 pada fungsi f(x) = x³ + 3x² sehingga diperoleh :

f(0) = 0 dan f(–2) = 4

Jadi, (0, 0) dan (–2,4) adalah titik-titik stasioner.

b. Interval fungsi naik diperoleh jika f '(x) > 0 dan interval fungsi turun diperoleh jika f '(x) < 0. Interval-interval tersebut diperoleh dengan menentukan nilai-nilai x yang disubstitusikan pada fungsi f ‘(x). Substitusikan x = –3 untuk x < –2, x = –1 untuk –2 < x < 0 dan x = 1 untuk x > 0 pada fungsi  f '(x) = 3x2 + 6x sehingga diperoleh :

f '(–3) = 9 > 0, f '(–1) = –3

f '(1) = 9 > 0

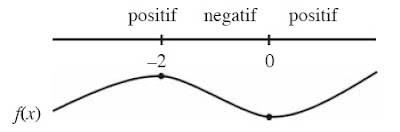
yang dapat digambarkan sebagai diagram di bawah ini :

f '(x) f '(–3) = 9 f '(–1) = –3 f '(1) = 9

Dari diagram tanda tersebut diperoleh interval berikut.

• Interval fungsi naik pada x < –2 dan x > 0.

• Interval fungsi turun pada –2 < x < 0.

c. Titik balik maksimum dan minimum lokal dapat ditentukan dari diagram tanda.

• Pada x = –2, f(x) berubah dari fungsi naik menjadi fungsi turun sehingga x = –2 adalah titik balik maksimum lokal.

f(x) = x³ + 3x² ↔ f(–2) = 4

Titik (–2, 4) adalah titik balik maksimum lokal.

• Pada x = 0, f(x) berubah dari fungsi turun menjadi fungsi naik sehingga x = 0 adalah titik balik minimum lokal f(x) = x³ + 3x² ↔ f(0) = 0

Titik (0, 0) adalah titik balik minimum lokal.

Langkah 3: Membuat sketsa grafik

Hasil sketsa grafik tampak pada Gambar di bawah ini.

 

Sumber:  http://www.nafiun.com/2014/06/cara-menggambar-grafik-fungsi-aljabar-pada-bidang-kartesius-menentukan-titik-potong-daerah-asal-nilai-fungsi-interval-fungsi-naik-dan-turun-titik-stasioner-belok.html