Hari, tanggal : Senin, 20 Januari 2020
Kelas : 8D-8G
Pengertian dari teorema pythagoras atau dalil phytagoras yaitu berbunyi :
Sisi miring atau sisi terpanjang dalam segitiga siku – siku sama dengan kuadrat sisi – sisi lainnya.
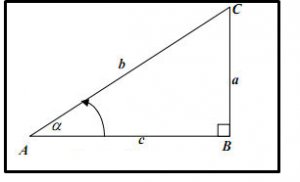
Perhatikan gambar di bawah ini :
Segitiga di atas merupakan segitiga siku-siku yang memiliki satu sisi tegak (BC), satu sisi mendatar (AB), dan satu sisi miring (AC).
Rumus Phytagoras (Pythagoras) :
b2 = a2 + c2
Maka untuk menghitung sisi tegak dan sisi mendatarnya berlaku rumus :
a2 = b2 – c2
c2 = b2 – a2
Rumus Pythagoras dalam bentuk akar
- Jika sisi miringnya c
- Sisi tegak dan mendatarnya adalah a dan b
Maka rumus pitagoras yang dihasilkan :
Catatan Penting : Rumus pythagoras, hanya berlaku pada segitiga siku – siku saja.
Teorema Phytagotas
Dalam dalil /teorema pythagoras, ada pola angka yang perlu untuk diingat supaya dalam menyelesaikan soal pythagoras akan lebih mudah dan cepat dalam mengerjakannya, pola tersebut adalah :
- 3 – 4 – 5
- 5 – 12 – 13
- 6 – 8 – 10
- 7 – 24 – 25
- 8 – 15 – 17
- 9 – 12 – 15
- 10 – 24 – 26
- 12 – 16 – 20
- 14 – 48 – 50
- 15 – 20 – 25
- 15 – 36 – 39
- 16 – 30 – 34
Untuk memahami lebih jelasnya mengenai dalil phytagoras, maka perhatikan contoh sebagai berikut
Contoh Soal Phytagoras dan Pembahasannya
Contoh Soal 1- Suatu segitiga siku- siku memiliki sisi tegak (AB) panjangnya 15 cm ,dan sisi mendatarnya (BC) 8 cm, berapakah cm kah sisi miringnya (AC) ?
Penyelesaian :
Diketahui :
AB = 15
BC = 8
AB = 15
BC = 8
Ditanya : Panjang AC …???
Jawab :
Cara pertama :AC2 = AB2 + BC2AC2 = 152 + 82AC2 = 225 + 64
AC2 = 289
AC = √289
AC = 17
AC2 = 289
AC = √289
AC = 17
Cara Kedua :AC = √ AB2 + BC2AC = √ 152 + 82AC = √ 255 + 64
AC = √ 289
AC = 17
AC = √ 289
AC = 17
Jadi, panjang AC adalah 17 cm
Contoh Soal 2- Berapakah panjang sisi tegak suatu segitiga siku – siku apabila diketahui panjang sisi miringnya 13 cm dan sisi datarnya 5 cm ?
Penyelesaiaannya :
Misal : c = sisi miring , b = sisi datar , a = sisi tegak
Diketahui : c = 13 cm , b = 5 cm
Ditanya : a = ….????
Jawab :
Cara Pertama :a2 = c2 – b2a2 = 132 – 52a2 = 169 – 25
a2 = 144
a = √ 144
a = 12
a2 = 144
a = √ 144
a = 12
Cara Kedua :a = √ c2 – b2a = √ 132 – 52a = √ 169 – 25
a = √ 144
a = 12
Jadi, panjang sisi tegak segitiga tersebut adalah 12 cm.
a = √ 144
a = 12
Jadi, panjang sisi tegak segitiga tersebut adalah 12 cm.
sumber : https://rumusrumus.com/rumus-dalil-pythagoras/
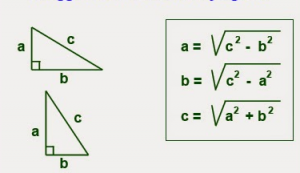


Tidak ada komentar:
Posting Komentar