HARI/TANGGAL;SENIN/4 JANUARI 2021

KELAS ; 9A

PAHAMI MATERI BERIKUT DAN KERJAKAN TUGASNYA KIRIM KE WA;082280107255.BERIKAN KOMENTAR MELALUI BLOGER MAUPUN SIMASKOT.

Kesebangunan dan Kekongruenan

Kesebangunan

Kesebangunan disimbolkan dengan ‘ ~ ‘ yang bisa dibaca sebangun. Misalkan diberikan dua buah bangun datar segitiga ABC dan segitiga DEF. Maka jika terdapat tulisan ∆ABC ~ ∆ DEF dapat diartikan bahwa dua buah segitiga tersebut sebangun.

  Dua
 buah bangun datar dikatakan sebangun jika memiliki besar sudut yang 
bersesuaian sama besar. Selain itu, perbandingan panjang sisi – sisi 
yang bersesuaian pada dua buah bangun datar tersebut juga sama.

Kesimpulannya, hubungan antara dua bangun datar dikatakan sebangun jika memenuhi syarat berikut.

1. Sudut – sudut yang bersesuaian sama besar (sudut – sudut – sudut)

2. Panjang sisi-sisi yang bersesuaian mempunyai perbandingan yang sama (sisi – sisi – sisi)

3. Dua sisi yang bersesuaian memiliki perbandingan yang sama dan sudut bersesuaian yang diapit sama besar (sisi – sudut – sisi)

Terdapat beberapa bentuk kesebangunan pada bidang datar, baik untuk bidang datar berbentuk segitiga atau bidang datar segi empat seperti pada trapesium. Berikut ini persamaan yang dihasilkan melalui kesebangunan pada kedua jenis bangun tersebut.

Kesebangunan pada Segitiga:

Bentuk 1: kesebangunan pada segitiga

$\frac{AD}{AB} = \frac{AE}{AC} = \frac{DE}{BC}$

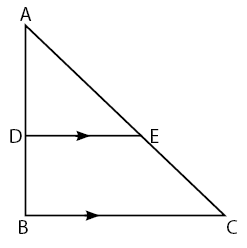
atau

$\frac{AD}{DB} = \frac{AE}{EC} =\frac{DE}{BC - DE}$

Bentuk 2: kesebangunan pada segitiga

$BC^{2} = CD \times CA$

$BA^{2} = AD \times AC$

$BD^{2} = DA \times DC$

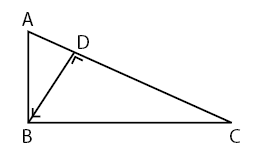
Berikutnya adalah kesebangunan pada bidang datar segi empat yaitu bangun datar berbentuk trapesium. Ada dua bentuk yang perlu di ketahui.

Kesebangunan pada Trapesium

Bentuk 1: kesebangunan pada trapesium

$EF = \frac{(DC \times AE) + (AB \times DE)}{AE + DE}$

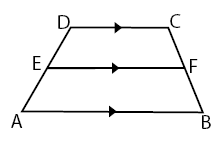
atau

$EF = \frac{(DC \times BF)+ (AB \times CF)}{CF + BF}$

Bentuk 2: kesebangunan pada trapesium

$EF =\frac{1}{2} \left(AB - CD \right)$

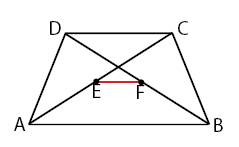
Keterangan: E dan F berturut-turut adalah titik tengah AC dan BD.

Kekongruenan

Dua benda atau lebih dikatakan kongruen jika memiliki bentuk dan ukuran yang sama. Dua buah bangun yang kongruen dihubungkan melalui simbol kongruen. Bagaimanakah simbol kongruen? Kekongruenan dilambangkan dengan $\cong$ .

Misalkan diberikan dua buah bangun segitiga yaitu ∆ABC dan ∆DEF. Kedua segitiga tersebut diketahui memiliki ukuran dan bentuk yang sama. Sehingga dapat dikatakan bahwa ∆ABC dan ∆DEF adalah kongruen. Penulisan yang menyatakan bahwa dua segitiga tersebut kongruen adalah ∆ABC $\cong$ ∆ DEF. Dibaca segitiga ABC kongruen dengan segitiga DEF.

Syarat Kekongruenan pada segitiga:

Sisi-sisi yang bersesuaian sama panjang (sisi – sisi – sisi)
Dua sisi yang bersesuaian sama panjang dan sudut yang diapit oleh kedua sisi tersebut sama besar (sisi – sudut – sisi)
Satu sisi dan dua sudut yang bersesuaian pada sisi itu sama besar (sudut – sisi – sudut)

Pelajari kekongruenan melalui contoh sederhana berikut. Perhatikan gambar segitiga di bawah!

Pasangan segitiga yang kongruen pada di atas tersebut adalah

$\Delta ABG \cong \Delta EDH$

$\Delta BGC \cong \Delta DHC$

$\Delta ABF \cong \Delta DFE$

$\Delta ACD \cong \Delta ECB$

$\Delta ABC \cong \Delta EDC$

$\Delta ABD \cong \Delta EDB$

$\Delta AGF \cong \Delta EHF$

$\Delta ACH \cong \Delta EGC$

Jadi, banyaknya segitiga yang kongruen ada 8 pasang.

Itulah tadi bahasan mengenai materi kesebangunan dan kekongruenan. Kesimpulan yang dapat diambil adalah, dua bangun datar yang sebangun belum tentu merupakan dua bangun datar yang saling kongruen. Namun, dua bangun datar yang kongruen pasti merupakan dua bangun datar yang sebangun.

Berikut ini penggunaan konsep kesebangunan untuk menyelesaikan berbagai permasalahan. Simak contoh soal kesebangunan dan pembahasan nya berikut.

Contoh Soal dan Pembahasan

Variasi soal pada kesebangunan dan kekongruenan sangat banyak. Berikut ini ada tiga tipe contoh soal yang keluar di Ujian Nasional beserta pembahasannya.

Contoh 1

Febri mempunyai tinggi badan 150 cm. Ia berdiri pada titik yang berjarak 10 m dari sebuah gedung. Ujung bayangan Febri berimpit dengan ujung bayangan gedung. Jika panjang bayangan Febri adalah 4 m, maka tinggi gedung adalah ….
A. 5,25 m
B. 5,50 m
C. 6,25 m
D. 6,75 m
SOAL UN MATEMATIKA SMP 2016

Pembahasan:

Perhatikan gambar berikut!

Perhatikan segitiga ABE dan segitiga ACD!

Berdasarkan prinsip kesebangunan dapat diperoleh

$\frac{EB}{DC} = \frac{AB}{AC}$

Sehingga,

$\frac{1,5}{DC} = \frac{4}{14}$

$DC = \frac{1,5 \times 14}{4}$

$DC = 5,25 \; m$

Jawaban: A

Contoh 2

Perhatikan gambar berikut!

Jika CF : FB = 2 : 3 dan CD = 12 cm, maka panjang EF adalah …. (SOAL UN MATEMATIKA SMP 2016)

A. 6 cm
B. 9 cm
C. 12 cm
D. 18 cm

Pembahasan:

Berdasarkan keterangan pada soal, kita dapat mengetahui ukuran masing-masing sisi, seperti terlihat pada gambar berikut.

Untuk menghitung EF, gunakan rumus di bawah.

$EF =\frac{CD \times FB + AB \times CF}{FB + CF}$

Sehingga,

$EF =\frac{12 \times 3x + 27 \times 2x}{3x + 2x}$

$EF =\frac{36x + 54x}{5x}$

$EF =\frac{90x}{5x}\;=\;18\;cm$

Jawaban: D

Contoh 3

“Lebar Sungai”

Andi ingin mengetahui lebar sungai. Di seberang sungai terdapat sebuah pohon. Untuk itu dia menancapkan tongkat sehingga berada pada posisi A, B, C, dan D dengan ukuran seperti pada gambar.