TEOREMA PYTHAGORAS

HARI/TANGGAL;JUMAT/8 JANUARI 2021

KELAS         :8D DAN 8E

PAHAMI MATERI BERIKUT DAN KERJAKAN TUGAS EVALUASI MANDIRI 1 HAL.164 NO.1A,1C,1D,2A,3A,4, DAN EVALUASI MANDIRI 2 HAL 167 NO.1A,1B,1C KIRIM KE WA;082280107255.BERIKAN KOMENTAR MELALUI BLOGGER MAUPUN SIMASKOT.SELAMAT BELAJAR.

 

 KONSEP YANG BERKAITAN DENGAN TEOREMA PYTHAGORAS

Dalil Pythagoras

Seorang nakhoda kapal melihat puncak mercusuar yang berjarak 80 meter dari kapal. Jika diketahui tinggi mercusuar adalah 60 meter dari permukaan laut, dapatkah kalian menentukan jarak nakhoda dari puncak mercusuar tersebut?

Persoalan di atas dapat kita hitung dengan menggunakan prinsip segitiga siku-siku. Jika panjang dua sisi segitiga siku-siku kita ketahui, maka sisi yang lain dapat kita tentukan. Caranya adalah dengan menggunakan dalil Pythagoras.

A. Pengertian Dalil Pythagoras

Dalam dalil Phytagoras melibatkan bilangan kuadrat dan akar kuadrat dalam sebuah segitiga.

Dalil Pythagoras adalah istilah lain dari teorema pythgoras yaitu bahwa sisi miring atau sisi terpanjang pada segitiga siku – siku sama dengan jumlah kuadrat sisi – sisi lainnya.

Oleh karena itu, sebelum membahas lebih jauh dalil Pythagoras, marilah kita mengingat kembali materi kuadrat bilangan, akar kuadrat bilangan, luas daerah persegi, dan luas daerah segitiga siku-siku.

1. Kuadrat dan Akar Kuadrat Bilangan

Masih ingatkah kalian bagaimana menentukan kuadrat dari suatu bilangan?

Untuk menentukan kuadrat dari suatu bilangan adalah dengan cara mengalikan bilangan tersebut dengan dirinya sendiri. 

Perhatikan contoh soal berikut ini

1.Tentukan kuadrat dari

a.5                  b.(-4)

Jawab:

a.( 5)2=5 x 5 =25                    b.(-4)2= (-4) x (-4) =16

2.Tentukan akar dari 

a.16

Jawab: v 16 = 4

Kebalikan dari kuadarat suatu bilangan adalah akar kuadrat. Misalkan, bilangan p yang tak negatif diperoleh p2 = 16. Maka bilangan p dapat ditentukan dengan menarik √16 menjadi p = √16. Bilangan p yang diinginkan adalah 4 karena 42 = 4 × 4 = 16. Bilangan p = 4 dinamakan akar kuadrat dari bilangan 16.

Jadi, akar kuadrat suatu bilangan adalah bilangan tak negatif yang apabila dikuadratkan akan menghasilkan bilangan yang sama dengan bilangan semula. 

2. Luas Daerah Persegi

Masih ingatkah kalian cara menentukan luas bangun datar persegi?

Luas persegi dapat ditentukan dengan cara mengalikan sisi-sisinya. 

Jika sisi sebuah persegi adalah s maka luasnya dapat dituliskan sebagai berikut.

L = s × s = s2

Perhatikan Contoh Soal Berikut!

Hitunglah luas persegi yang panjang sisinya 6 cm

Jawab: Panjang sisi 6 cm maka s=6cm

L= s x s = 6 x 6 = 36 cm2

3. Luas Daerah Segitiga

Kalian tentu sudah mempelajari cara menghitung luas dan keliling segitiga. Pada pembahasan ini kalian akan mempelajari hubungan antara luas segitiga dengan luas persegi panjang.

Dari persegi panjang tersebut kita memperoleh dua buah segitiga, yaitu ΔPQR dan ΔPSR. Luas ΔPQR = luas daerah ΔPSR.

Hal ini menunjukkan bahwa:

Luas ΔPQR = ½ × luas PQRS
                    = ½ × panjang PQ × panjang QR
                    = ½ × alas × tinggi

Jadi, luas segitiga dirumuskan:

L = ½ × a × t

Keterangan:
a = alas segitiga, dan
t = tinggi segitiga

Perhatikan contoh soal berikut!

Hitunglah luas segitiga jika diketahui alasnya 9 cm dan tingginya 6 cm.

Jawab: L = 1/2 x a x t = 1/2 x 9 x 6 = 27 cm2

B. Pembuktian Dalil Pythagoras

Luas persegi dan segitiga yang dibahas di atas dapat digunakan untuk menenemukan dalil Pythagoras.

Untuk menemukan dalil Pythagoras lakukanlah kegiatan berikut ini!

Berdasarkan kegiatan di atas kalian akan memperoleh sifat segitiga siku-siku, yaitu pada setiap segitiga siku-siku, kuadrat sisi miring sama dengan jumlah kuadrat sisi siku-sikunya. Sifat inilah yang kemudian dikenal dengan dalil Pythagoras.

 Jadi, jika ABC adalah sembarang segitiga siku-siku dengan panjang sisi siku-siku a dan b serta panjang sisi miring c maka berlaku hubungan sebagai berikut:

c2 = a2 + b2

C. Penerapan Dalil Pythagoras

Dengan menggunakan dalil Pythagoras, kalian dapat menentukan panjang salah satu sisi segitiga siku-siku jika diketahui dua sisi yang lainnya.

Selain itu, dalil ini dapat digunakan juga untuk menentukan jenis segitiga dengan membandingkan kuadrat sisi miringnya dengan jumlah kuadrat sisi siku-sikunya.

Untuk lebih jelasnya, penerapan dalil Pythagoras dapat digunakan untuk hal-hal berikut ini:

1. Menghitung panjang salah satu sisi segitiga siku-siku
2. Menentukan jenis segitiga jika diketahui panjang sisi-sisinya
3. Menghitung perbandingan sisi-sisi segitiga khusus
4. Menentukan panjang diagonal sisi dan diagonal ruang kubus

Penjelasan lebih lengkap untuk penerapan dalil pythagoras adalah;

1. Menghitung Panjang Salah Satu Sisi Segitiga Siku-Siku

Pada sebuah segitiga siku-siku, jika dua buah sisinya diketahui maka salah satu sisinya dapat dicari dengan menggunakan dalil Pythagoras.

Perhatikan contoh soal berikut ini!

Diketahui segitiga siku-siku ABC dengan siku-siku di B yang digambarkan sebagai berikut:

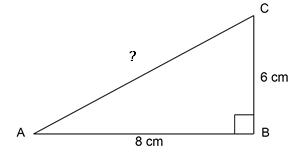
Tentukan panjang sisi miring AC pada gambar di atas!

Jawab:

Sebab segitiga di atas adalah segitiga siku-siku, maka berlaku rumus Phytagoras seperti betikut ini:

AC² = AB² + BC²
AC² = 8² + 6²
AC² = 64 + 36
AC² = 100
AC  =  √100
AC  = 10

Sehingga, panjang sisi AC dalam segitiga siku-siku tersebut yaitu 10 cm.

Soal 2.

Suatu segitiga siku-siku KLM dengan siku-siku di L digambarkan seperti di bawah ini:

Tentukan panjang sisi KL pada gambar di atas!

Jawab:

Sebab, segitiga di atas adalah segitiga siku-siku, maka berlaku rumus Phytagoras seperti berikut ini:

KM² = KL² + LM²
KL² = KM² – LM²
KL² = 13² – 12²
KL² = 169 – 144
KL² = 25
KL  =  √25
KL = 5

Sehingga, panjang sisi KL dalam segitiga siku-siku di atas yaitu 5 cm.

Soal 3.

Diketahui segitiga siku-siku DEF dengan siku-siku di E digambarkan seperti di bawah ini:

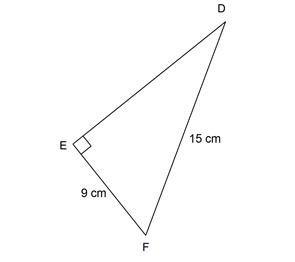
Tentukan panjang sisi DE pada gambar di atas!

Jawab:

Sebab segitiga DEF di atas merupakan segitiga siku-siku, maka berlaku rumus Phytagoras seperti di bawah ini:

DF² = DE² + EF²
DE² = DF² – EF²
DE² = 15² – 9²
DE² = 225 – 81
DE² = 144
DE  =  √144
DE = 12

Sehingga, panjang sisi DE pada segitiga siku-siku di atas yaitu 12 cm.

Soal 4.

Diketahui segitiga siku-siku ABC dengan siku-siku berada di B. Apabila panjang sisi AB = 16 cm serta Panjang sisi BC = 12 cm.

Maka hitunglah panjang sisi AC pada segitoga di atas!

Jawab:

Dari soal di atas bisa kiat gambarkan sebuah segitiga siku-siku seperti berikut ini:

Sebab segitiga di atas adalah segitiga siku-siku, maka berlaku rumus Phytagoras seperti di bawah ini:

c² = a²  + b²
c² = 12² + 16²
c² = 144 + 256
c² = 400
c = √400
c = 20

Sehingga, panjang sisi AC pada segitiga siku-siku ABC dalam soal di atas yaitu 20 cm